Subjects:
- Series and parallel circuits in general
- Series connection in practice
- Series Connection: Calculating Replacement Resistance
- Series connection: calculating current and partial voltage
- Parallel Connection: Calculating Replacement Resistance
- Parallel connection: calculating partial currents
- Combined circuit
- Combined circuit exercise
Series and parallel circuits in general:
On this page we look at series circuits, parallel circuits and combined circuits that are used in automotive technology. The knowledge of the basic electronics is required for this.
Series connection:
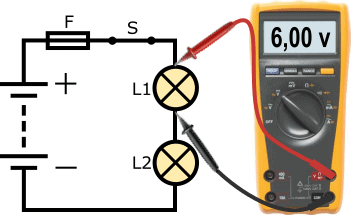
The following circuit shows a circuit with a 12 volt battery, a fuse (F), closed switch (S) and two lamps (L1 and L2). The negative wire of lamp L1 is connected to the positive wire of lamp L2. We call this a series circuit.
The current through both lamps is the same. The tension is distributed. Since two lamps of the same power were used in the example, the battery voltage of 12 volts divides into 6 volts per lamp. For this reason, lamps in automotive technology are not placed in series. Also, in the case of one defective lamp, the complete circuit will be interrupted, so that the other lamp will no longer burn.
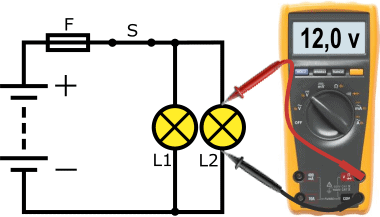
Parallel connection:
In automotive technology, we are almost always dealing with parallel circuits. The following circuit shows the circuit in which the lamps L1 and L2 both have their own positive and ground wire. The voltage across each consumer is equal to the battery voltage; this can be seen in the volt measurement. In this example, the same lamps are used as in the series connection; here, however, they burn brighter because the lamps now receive more voltage and current.
Another property of a parallel circuit is that when one lamp is defective, it does not affect the operation of the other lamp.
Series connection in practice:
As described in the previous section, in automotive technology we are almost always dealing with consumers connected in parallel. After all, we want as much voltage and current as possible to make the consumers work, and as little risk as possible of malfunctions if one of the consumers breaks down.
In practice, we find consumers that are placed in series to perform their task. Let's take the interior fan / heater motor as an example. In order to be able to regulate the speed of the fan, a resistor is placed in series in the ground connection between the electric motor and the ground point. We also call this a series resistor.
By placing one or more resistors in series, the loss increases and the voltage across the electric motor decreases.
Read more about this on the page: ballast resistor of the passenger compartment fan.
An unwanted series connection may also be present; for example, a contact resistance in a positive or ground connection with a voltage drop as a result (see the page “measure with the multimeter").
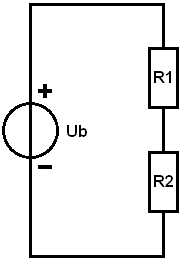
Series Connection: Calculating Replacement Resistance:
Every electrical consumer has an internal one resistance. A high resistance results in a low current; in other words: the resistance determines the current. The supplied voltage is equal to the source voltage (Ub, or battery voltage).
In the example, the consumers (R1 and R2) are connected in series. The minus of R1 is connected to the plus of R2. The current through the resistors is equal. In order to calculate the current and finally the partial voltages using Ohm's Law, we can start by calculating the replacement resistance. The resistance values are as follows:
- R1 = 15
- R2 = 10
To calculate the replacement resistance, in the scheme we replace the resistors R1 and R2 with Rv.
In a series circuit, we can add the resistance values together. The formula and elaboration are shown below.
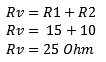
The result of the calculation shows us that the replacement resistance is 25 Ohms. In the following examples we can continue to calculate with the Rv.
Series connection: calculating current and partial voltages:
In this section we calculate the total current and the partial voltages across the resistors R1 and R2. To start with, we need a source voltage (Ub). In this calculation example, this voltage is 14 volts.
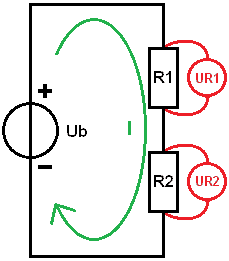
With a known source voltage (Ub) and replacement resistance (Rv) we can calculate the total current (I). We determine the I with the Ohm's Law:
The current in a series circuit is the same through every resistor. The green arrow in the figure indicates the flow direction. The current is 560 milliamps.
Now that the current is known, we can calculate the partial voltages. We use this to determine how much voltage each resistor “consumes”.
- The voltage (U) across the resistor R1 is denoted as: UR1. Using Ohm's Law we multiply the current by the resistance value. The voltage across the resistor is 8,4 volts.
- We calculate UR2 with the same current, but now with the resistance value of R2; this voltage is 5,6 volts.
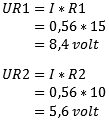
To check, you can add the partial voltages together and compare them with the source voltage. We add UR1 and UR2 together: this is 14 volts. This is equal to the source voltage. If you arrive at a different answer, a small deviation may be due to an interim rounding or an error in the calculation.
Parallel Connection: Calculating Replacement Resistance:
In this example, R1 and R2 are connected in parallel. Now the minus of one consumer is no longer connected with the plus of the other. The voltage across the resistors is now equal to the battery voltage. The current is distributed across the resistors. With equal resistance values, the total current (I total, abbreviated as It) divides by two. To calculate It, we must first determine the replacement resistance. Again we replace R1 and R2 with one resistor, called Rv. We then get the same situation as in the example with the series connection. The resistance values are:
- R1 = 10
- R2 = 20
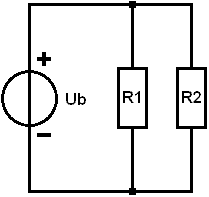
In a parallel circuit, we cannot add up the resistance values. The general formula is:
We fill in the resistance values of R1 and R2:
Way 1: We calculate the result of a tenth and a twentieth and add the values together.
Way 2: Another way is to calculate the replacement resistance in fraction form. We fill in the values of R1 and R2 again in the equation. Below the hyphens (the denominators) are unequal numbers; we cannot add the denominators together. That is why we first make them the same name. In this example, it's easy: a tenth fits into a twentieth twice, so we multiply a tenth in its entirety by 2. We get two-twentieth. In proportion, that's the same as one-tenth. With like denominators we can add the fraction: this results in third-twentieth. To calculate the replacement resistance we need to reverse the fraction: 1/RV becomes RV/1 (we can then cross out /1) and third-twentieth becomes 20 divided by 3. The result of 6,67 Ohm is equal to the result of way 1.
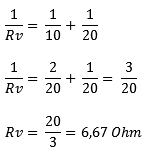
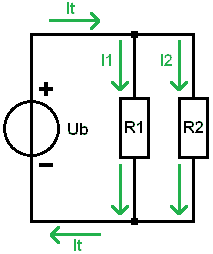
Parallel connection: calculating partial currents:
We can calculate the total current (It) by dividing Ub and Rv by each other:
The current Itotaal will divide into I1 and I2. A different current flows through R1 than through R2. At the node, the partial currents come together again and it runs to the negative of the battery again.
In a parallel circuit, the following applies: the voltage across each consumer is equal to the source voltage:
In the formulas at UR1 and UR2, we therefore enter the same value as the battery voltage: in this case 14 volts. We divide the voltage by the resistance values and obtain the partial currents. A current of 1 amps flows through resistor R1,4 and 2 milliamps through R700.
When we add the two partial currents together, we again get the total current of 2,1 Ampere.
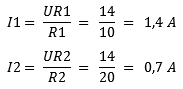
Combined circuit:
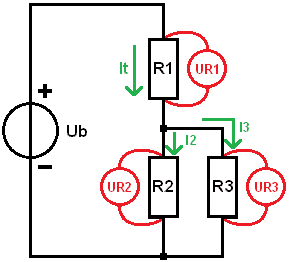
In a combined circuit, we are dealing with a series and parallel circuit in one circuit. In the figure we see that the resistor R1 is in series with the parallel-connected resistors R2 and R3. In practice we could find this with a bad positive wire to two lamps: R1 in that case is the contact resistance, R2 and R3 are the lamps.
We are going to calculate the currents and voltages based on the following data:
- Ub = 12 volts;
- R1 = 0,5
- R2 = 15
- R3 = 15
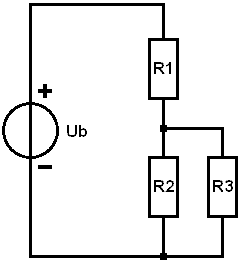
From a parallel circuit we know that the voltage across the resistors is equal to the source voltage. Because we are now dealing with a combined circuit, this no longer applies; part is taken up by R1. However, the voltages across R2 and R3 are equal to each other.
For clarity, we divide the calculations into 5 steps.
1. Determine Rv of the parallel circuit:
We replace R2 and R3 with Rv and calculate Rv in fraction form for convenience.
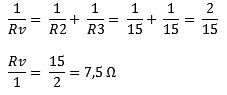
Now there is a series connection: R1 remains of course 0,5 and Rv is now 7,5
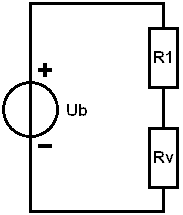
2. Determine Rv of the series connection:
In step 1, the replacement resistance of R2 and R3 is determined. The replacement resistor was in series with resistor R1.
In this step we add the resistance values of R1 and Rv together to calculate the replacement resistance again, this time that of the series connection. We call this replacement resistor: Rv' (with an accent) because it is a “second” Rv in the circuit.
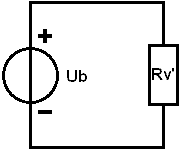
3. Calculate Itotal:
The total current is 1,5 A and flows through the resistor R1 and the replacement resistor Rv'.
4. Calculating partial voltages:
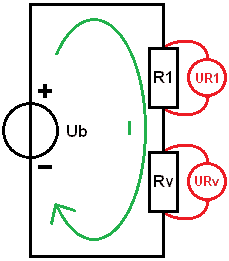
We build the scheme back step by step; we put R1 and Rv in series to calculate the partial voltages UR1 and URv with the total current and resistance values.
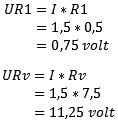
As a check: the partial voltages added together correspond to the source voltage: (UR1 + URv = Ub) so no calculation errors have been made so far.
5. Calculating Flows:
We will complete the schedule again. In step 4 we determined that the voltage across resistor R1 is 0,75 volts. The voltage across the replacement resistor Rv is 11,25 volts. Since the voltage across the consumers is the same in a parallel circuit, we know that the voltage across both R2 and R3 is 11,25 volts.
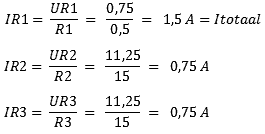
The results of the calculations show that the total current flows through R1, and the current then divides itself between R2 and R3. With unequal resistance values, these currents differ from each other.
Combined circuit exercise:
In this section you can practice calculating on the combined circuit yourself. To make it easy on yourself, you can follow steps 1 to 5 from the previous paragraph. Extend the step-by-step plan with step 6 to calculate the partial voltages of R4 and R5.
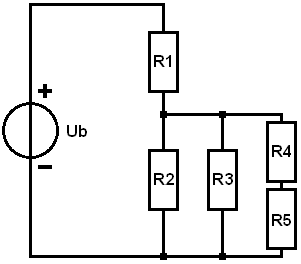
Given:
- Ub = 10 volts
- R1 = 1
- R2 = 10
- R3 = 4
- R4 = 5
- R5 = 15
Asked:
- All partial voltages (UR1 to UR5)
- All partial flows.
