Tárgyak:
- Soros és párhuzamos áramkörök általában
- Soros kapcsolat a gyakorlatban
- Soros csatlakozás: számítsa ki a csereellenállást
- Soros csatlakozás: áram és részfeszültség kiszámítása
- Párhuzamos csatlakozás: számítsa ki a csereellenállást
- Párhuzamos csatlakozás: részáramok kiszámítása
- Összetett áramkör
- Kombinált körgyakorlat
Soros és párhuzamos áramkörök általában:
Ezen az oldalon az autóiparban használt soros, párhuzamos és kombinált áramköröket tekintjük át. A tudás a alapvető elektronika szükséges ehhez.
Soros csatlakozás:
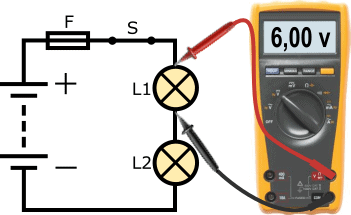
A következő áramkör egy 12 voltos akkumulátorral, egy biztosítékkal (F), zárt kapcsolóval (S) és két lámpával (L1 és L2) rendelkező áramkört mutat be. Az L1 lámpa negatív vezetéke az L2 lámpa pozitív vezetékéhez csatlakozik. Ezt hívjuk soros kapcsolatnak.
Az áramerősség mindkét lámpán azonos. A feszültség megoszlik. Mivel a példában két azonos teljesítményű lámpát használtunk, a 12 voltos akkumulátorfeszültség lámpánként 6 voltra oszlik. Emiatt az autóipari lámpák nem kerülnek sorozatba. Ezenkívül, ha az egyik lámpa meghibásodik, a teljes áramkör megszakad, ami miatt a másik lámpa nem ég tovább.
Párhuzamos csatlakozás:
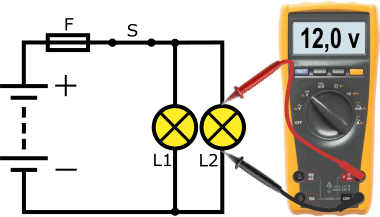
Az autóiparban szinte mindig párhuzamos áramkörökkel foglalkozunk. A következő áramkör azt az áramkört mutatja, amelyben az L1 és L2 lámpáknak saját pozitív és testvezetéke van. Az egyes fogyasztók feszültsége megegyezik az akkumulátor feszültségével; ez látszik a volt mérésen. Ebben a példában ugyanazokat a lámpákat használjuk, mint a soros csatlakozásnál; Itt azonban fényesebben égnek, mert a lámpák most több feszültséget és áramot kapnak.
A párhuzamos áramkör másik tulajdonsága, hogy ha az egyik lámpa meghibásodik, az nem befolyásolja a másik lámpa működését.
Soros kapcsolat a gyakorlatban:
Az előző bekezdésben leírtak szerint az autótechnikában szinte mindig párhuzamosan kapcsolt fogyasztókkal foglalkozunk. Hiszen a lehető legtöbb feszültséget és áramerősséget szeretnénk elérni, hogy a fogyasztók dolgozhassanak, és minél kisebb a meghibásodás veszélye, ha valamelyik fogyasztó meghibásodik.
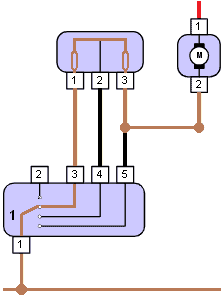
A gyakorlatban olyan fogyasztókat találunk, akiket sorba helyeznek a feladatuk ellátására. Példaként vesszük a belső ventilátor/fűtőmotort. A ventilátor fordulatszámának szabályozására az elektromos motor és a földelési pont közötti földcsatlakozásban sorba sorba kell helyezni egy ellenállást. Ezt soros ellenállásnak is hívjuk.
Egy vagy több ellenállás sorba állítása esetén a veszteség növekszik és az elektromos motor feszültsége csökken.
Erről bővebben a következő oldalon olvashat: az utastér ventilátorának soros ellenállása.
Nem kívánt soros kapcsolat is előfordulhat; például átmeneti ellenállás pozitív vagy földelő csatlakozásban, ami feszültségveszteséget okoz (lásd a "mérje meg a multiméterrel").
Soros csatlakozás: csereellenállás kiszámítása:
Minden elektromos fogyasztónak van belső fogyasztója ellenállás. A nagy ellenállás alacsony áramerősséget eredményez; más szóval: az ellenállás határozza meg az áramerősséget. A betáplált feszültség megegyezik a forrásfeszültséggel (Ub vagy akkumulátorfeszültség).
A példában a fogyasztók (R1 és R2) sorba vannak kötve. R1 negatívja R2 pozitívjához kapcsolódik. Az ellenállásokon áthaladó áram egyenlő. Az áramerősség és végső soron a parciális feszültségek Ohm törvénye alapján történő kiszámításához kezdhetjük a csereellenállás kiszámításával. Az ellenállási értékek a következők:
- R1 = 15 Ω
- R2 = 10 Ω
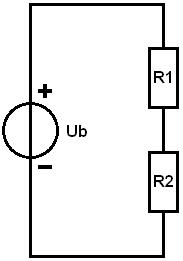
A csereellenállás kiszámításához a diagramban szereplő R1 és R2 ellenállásokat Rv-re cseréljük.
Soros áramkörben összeadhatjuk az ellenállásértékeket. A képlet és a hatás az alábbiakban látható.
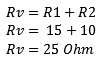
A számítás eredménye azt mutatja, hogy a csereellenállás 25 Ohm. A következő példákban tovább számolhatunk az Rv-vel.
Soros csatlakozás: áram- és részfeszültségek kiszámítása:
Ebben a részben kiszámítjuk a teljes áramot és az R1 és R2 ellenállásokon lévő részfeszültségeket. Először is szükségünk van egy forrásfeszültségre (Ub). Ebben a számítási példában ez a feszültség 14 volt.
Ismert forrásfeszültséggel (Ub) és csereellenállással (Rv) kiszámíthatjuk a teljes áramot (I). Meghatározzuk az I-t a Ohm törvénye:
A soros áramkörben az áram minden ellenálláson azonos. Az ábrán látható zöld nyíl az áramlás irányát jelzi. Az áramerősség 560 milliamper.
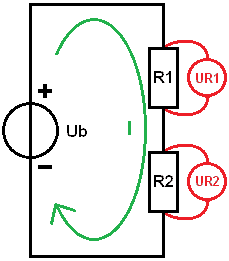
Most, hogy az áramerősség ismert, kiszámolhatjuk a részfeszültségeket. Ezt használjuk annak meghatározására, hogy az egyes ellenállások mekkora feszültséget „fogyasszanak”.
- Az R1 ellenálláson lévő feszültséget (U) UR1-nek nevezzük. Az Ohm-törvény segítségével megszorozzuk az áramerősséget az ellenállás értékével. Az ellenálláson lévő feszültség 8,4 volt.
- Az UR2-t ugyanazzal az áramerősséggel számoljuk, de most az R2 ellenállásértékkel; ez a feszültség 5,6 volt.
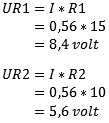
Az ellenőrzéshez összeadhatja a részfeszültségeket, és összehasonlíthatja őket a forrásfeszültséggel. Összeadjuk az UR1-et és az UR2-t: ez 14 volt. Ez egyenlő a forrásfeszültséggel. Ha más válaszra jut, ennek oka lehet a közbenső kerekítésből adódó kis eltérés vagy a számítás hibája.
Párhuzamos csatlakozás: csereellenállás kiszámítása:
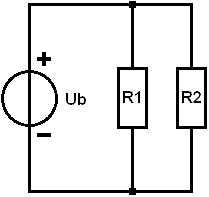
Ebben a példában R1 és R2 párhuzamosan kapcsolódnak. Most az egyik fogyasztó mínusza már nem kapcsolódik a másik pluszhoz. Az ellenállásokon lévő feszültség ekkor egyenlő az akkumulátor feszültségével. Az áramerősség eloszlik az ellenállásokon. Egyenlő ellenállásértékek esetén a teljes áram (I total, rövidítve It) osztódik kettővel. Ennek kiszámításához először meg kell határoznunk a helyettesítési ellenállást. Ismét lecseréljük az R1-et és az R2-t egy ellenállásra, az úgynevezett Rv-re. Ekkor ugyanazt a helyzetet kapjuk, mint a példában a soros kapcsolással. Az ellenállási értékek a következők:
- R1 = 10 Ω
- R2 = 20 Ω
Párhuzamos áramkörben nem tudjuk összeadni az ellenállásértékeket. Az általános képlet a következő:
Beírjuk az R1 és R2 ellenállásértékeit:
1. út: Kiszámoljuk a tized és a huszad eredményét, és összeadjuk az értékeket.
2. út: Egy másik módszer a helyettesítési ellenállás tört alakban történő kiszámítása. Ismét beírjuk az R1 és R2 értékeit az egyenletbe. Az osztóvonalak (a nevezők) alatt egyenlőtlen számok vannak; nem tudjuk összeadni a nevezőket. Ezért először névadóvá tesszük őket. Ebben a példában ez egyszerű: egy tized kétszer megy a huszadba, tehát egy egész tizedet megszorozunk 2-vel. Ekkor kapunk kéthuszadot. Arányában ez megegyezik az egytizedével. Ugyanazokkal a nevezőkkel összeadhatjuk a törtet: ez háromhuszadot eredményez. A csereellenállás kiszámításához meg kell fordítanunk a törtet: 1/RV-ből RV/1 lesz (ezután /1-et kihúzhatunk), és a három huszadból 20 osztva 3-mal. A 6,67 Ohm eredmény egyenlő az 1. út eredményével. .
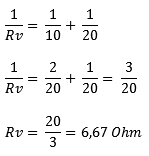
Párhuzamos csatlakozás: számítsa ki a részáramokat:
A teljes áramot (It) úgy számíthatjuk ki, hogy Ub-t és Rv-t elosztjuk egymással:
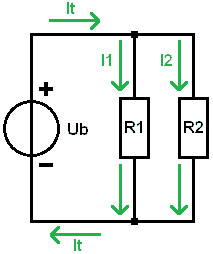
A jelenlegi Itotaalt I1-re és I2-re osztják. Az R1-en más áram folyik, mint az R2-n. Az elágazásnál a részáramok ismét összeérnek, és az akkumulátor negatív oldalára fut vissza.
Párhuzamos kapcsolásnál az egyes fogyasztók feszültsége megegyezik a forrásfeszültséggel:
Az UR1 és UR2 képletébe az akkumulátor feszültségével megegyező értéket írunk be: ebben az esetben 14 volt. A feszültséget elosztjuk az ellenállásértékekkel, és megkapjuk a részáramokat. Az R1 ellenálláson 1,4 amper, az R2 ellenálláson pedig 700 milliamper áram folyik át.
Ha a két részáramot összeadjuk, akkor a teljes áramerősség 2,1 amper.
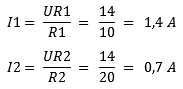
Összetett áramkör:
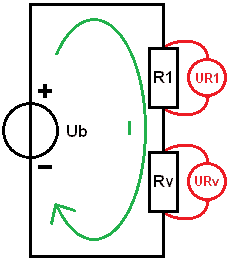
Kombinált áramkörrel soros és párhuzamos áramkörrel van dolgunk egy áramkörben. Az ábrán azt látjuk, hogy az R1 ellenállás sorba van kapcsolva a párhuzamosan kapcsolt R2 és R3 ellenállásokkal. Gyakorlatilag két lámpa rossz pozitív vezetékével találkozhatunk: R1 ebben az esetben az átmeneti ellenállás, R2 és R3 a lámpák.
Az áramokat és feszültségeket a következő adatok alapján számítjuk ki:
- Ub = 12 volt;
- R1 = 0,5 Ω
- R2 = 15 Ω
- R3 = 15 Ω
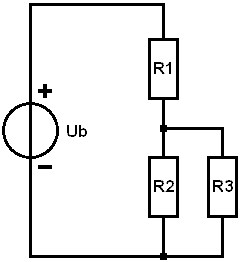
Párhuzamos áramkörben tudjuk, hogy az ellenállásokon lévő feszültség megegyezik a forrásfeszültséggel. Mivel most egy kombinált áramkörről van szó, ez már nem érvényes; egy részét R1 veszi fel. Az R2 és R3 feszültsége azonban egyenlő.
Az érthetőség kedvéért a számításokat 5 lépésre osztjuk.
1. Határozza meg a párhuzamos csatlakozás Rv értékét:
Az R2-t és az R3-at Rv-re cseréljük, és az Rv-t tört formában számítjuk ki a kényelem kedvéért.
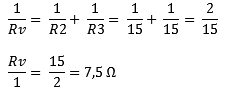
Most soros kapcsolat van: R1 nyilvánvalóan 0,5 Ω marad, Rv pedig 7,5 Ω
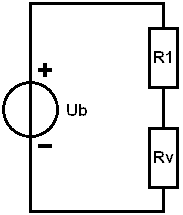
2. Határozza meg a soros csatlakozás Rv értékét:
Az 1. lépésben meghatároztuk az R2 és R3 helyettesítési ellenállását. A csereellenállás sorba kapcsolt az R1 ellenállással.
Ebben a lépésben összeadjuk az R1 és Rv ellenállásértékeit, hogy ismét kiszámítsuk a csereellenállást, de most a soros áramkörét. Ezt a csereellenállást Rv'-nek hívjuk (ékezettel), mert ez a „második” Rv az áramkörben.
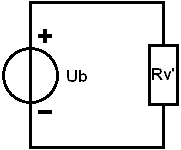
3. Számítsa ki az összeget:
A teljes áram 1,5 A, és az R1 ellenálláson és az Rv' csereellenálláson keresztül folyik.
4. Számítsa ki a részfeszültségeket:
Lépésről lépésre újjáépítjük a sémát; sorba állítjuk az R1 és Rv értékeket, hogy kiszámítsuk az UR1 és URv részfeszültségeket a teljes áram- és ellenállásértékekkel.
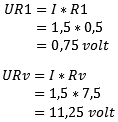
Ellenőrizendő: a részfeszültségek összeadva megfelelnek a forrásfeszültségnek: (UR1 + URv = Ub), így számítási hiba eddig nem történt.
5. Számítsa ki az áramlásokat:
Ismét teljesítjük a menetrendet. A 4. lépésben megállapítottuk, hogy az R1 ellenálláson lévő feszültség 0,75 volt. Az Rv csereellenállás feszültsége 11,25 volt. Mivel párhuzamos áramkörben a fogyasztók feszültsége azonos, tudjuk, hogy az R2 és R3 feszültsége 11,25 volt.
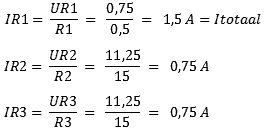
A számítások eredményei azt mutatják, hogy a teljes áram átfolyik az R1-en, majd az áram eloszlik R2 és R3 között. Egyenlőtlen ellenállásértékek esetén ezek az áramok különböznek egymástól.
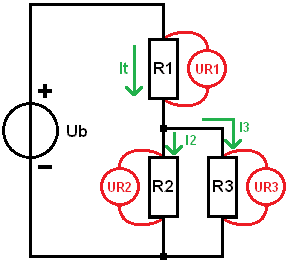
Kombinált körgyakorlat:
Ebben a részben saját maga gyakorolhatja a kombinált áramkör kiszámítását. Hogy megkönnyítse a dolgát, kövesse az előző bekezdés 1–5. lépéseit. Az R6 és R4 részfeszültségének kiszámításához bontsa ki a lépésenkénti tervet a 5. lépéssel.
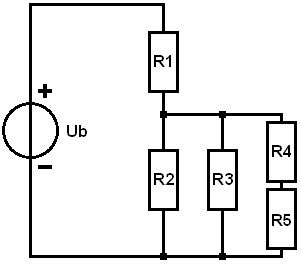
Datum:
- Ub = 10 volt
- R1 = 1 Ω
- R2 = 10 Ω
- R3 = 4 Ω
- R4 = 5 Ω
- R5 = 15 Ω
kérte:
- Minden részfeszültség (UR1-től UR5-ig)
- Minden alfolyam.
