Tárgyak:
- bevezetés
- Wheatstone híd egyensúlyban
- Kiegyensúlyozatlan híd Wheatstone-ból (az ellenállási értékek ismertek)
- Wheatstone híd ismeretlen ellenállás értékkel
Bevezetés:
A Wheatstone-híd egy elektromos hídáramkör az állandó vagy változó elektromos ellenállás pontos mérésére. Ez az áramkör fizikai mennyiségek, például hőmérséklet és nyomás mérésére használható, amint azt a légtömeg mérő (a forró vezeték hőmérséklete) és MAP érzékelő (nyomás a szívócsonkban).
Wheatstone hídjában négy van ellenállások, amelyek közül háromnak ismert, egynek pedig ismeretlen az ellenállása. A híd tulajdonképpen két párhuzamosan kapcsolt feszültségosztóból áll.
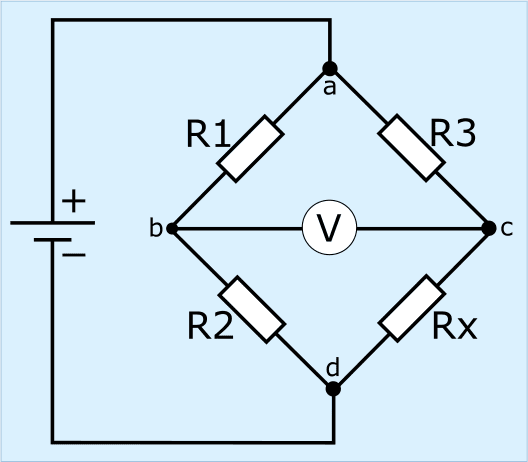
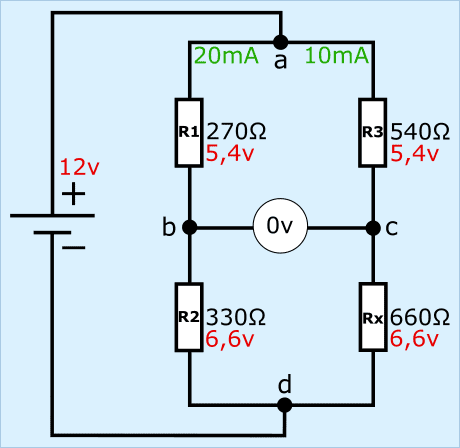
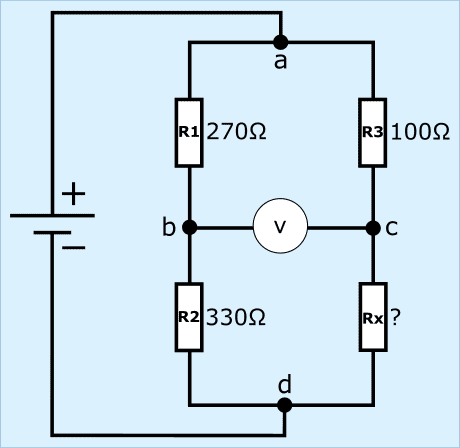
A képen az R1–R3 (ismert ellenállásértékek) és Rx (ismeretlen) ellenállásokat látjuk, a két feszültségosztó közepén egy voltmérővel, a hídtól balra pedig egy feszültségforrással.
A Wheatstone-híd kiegyensúlyozott, ha a b és c pontok közötti kimeneti feszültség 0 volt. A következő bekezdések különböző helyzeteket mutatnak be.
Wheatstone híd egyensúlyban:
A Wheatstone-híd kiegyensúlyozott vagy kiegyensúlyozott, ha a kimeneti feszültség 0 volt, mivel a bal és jobb oldali ellenállásértékek arányosak egymással.
Az áramkör ebben a szakaszban másképp van megrajzolva, mint az előző részben, de ugyanazon a műveleten alapul.
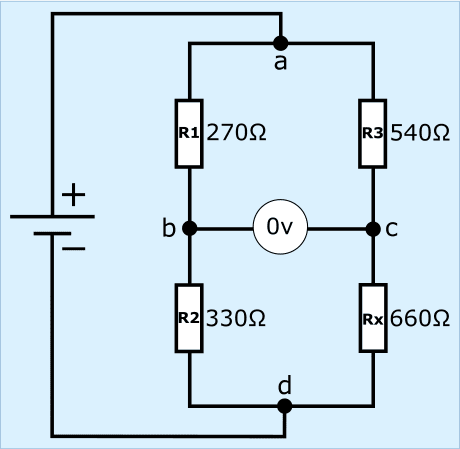
- az R1 és R2 ellenállások ellenállása 270 és 330 Ω. Összeadva ez 600 Ω;
- az R3 és Rx ellenállások 540 és 660 Ω ellenállásúak. Ez összeadva 1200 Ω.
A bal és jobb oldali ellenállások aránya azonos. Ez azt jelenti, hogy az ellenállási arányok és a feszültségesések egyenlőek R1 és R3, valamint R2 és Rx között.
Az alábbi képletek az egyenlő ellenállás-arányokat és a feszültségeséseket mutatják:
![]() en
en ![]()
Ismert tápfeszültség és ellenállás értékekkel meg tudjuk határozni az ellenállásokon áthaladó feszültségeséseket, így a b és c pontok közötti feszültségkülönbséget. Az alábbi példában kiszámítjuk a b és c pontok közötti feszültségkülönbséget egy kiegyensúlyozott Wheatstone-hídra. A tudás a Ohm törvénye és számolj azzal soros és párhuzamos áramkörök követelmény.
1. Számítsa ki az R1 és R2 ellenállásokon keresztüli áramokat (RV = csereellenállás):
![]()
2. Számítsa ki a feszültségesést az R1 és R2 ellenállásokon:
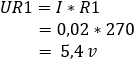
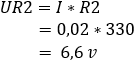
3. Számítsa ki az R1 és R2 ellenállásokon átmenő áramokat:![]()
4. Számítsa ki a feszültségesést az R3 és Rx ellenállásokon:
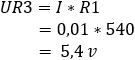
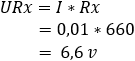
A b és c pontokban a feszültség 5,4 volt. A potenciálkülönbség 0 volt.
Kiegyensúlyozatlan híd Wheatstone-ból (az ellenállási értékek ismertek):
Az Rx ellenállásának változása következtében a Wheatstone-híd kiegyensúlyozatlanná válik. Az ellenállásváltozás bekövetkezhet például változó hőmérséklet miatt, ahol Rx a termisztor van. Az R1 és R2 közötti feszültségosztó változatlan marad, de az R3 és Rx között nem. Mivel a feszültségosztó ott változik, a c pontban más feszültséget kapunk. Ebben a példában az Rx ellenállásértéke 600 Ω-ról 460 Ω-ra csökkent.
1. Számítsa ki az R1 és R2 ellenállásokon keresztüli áramokat:
![]()
2. Számítsa ki a feszültségesést az R1 és R2 ellenállásokon:
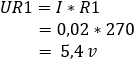
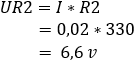
4. Számítsa ki a feszültségesést az R3 és Rx ellenállásokon:
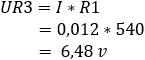
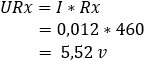
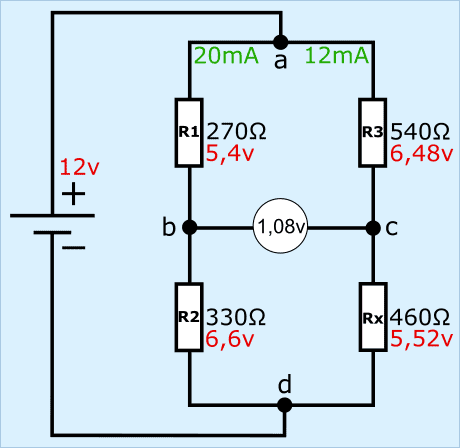
A két példában az Rx ellenállásértéke 660 Ω-ról 460 Ω-ra változott. Ez az ellenállásváltozás hatására a bc közötti feszültség 0 voltról 1,08 voltra változott. Ha ez a Wheatstone-híd be van építve az érzékelő elektronikájába, akkor az 1,08 voltos feszültség jelfeszültségnek tekinthető. Ezt a jelfeszültséget egy jelvezetéken keresztül továbbítják az ECU-hoz. A A/D konverter az ECU-ban az analóg feszültséget digitális üzenetté alakítja, amelyet a mikroprocesszor ki tud olvasni.
Wheatstone híd ismeretlen ellenállási értékkel:
Az előző részekben ismert Rx ellenállásértéket feltételeztünk. Mivel ez az ellenállásérték változó, tovább mehetünk, és kiszámíthatjuk ezt az ellenállásértéket a Wheatstone-híd kiegyensúlyozására.
Ebben az áramkörben R1 és R2 ismét 270 és 330 Ω. Az R3 ellenállása 100 Ω-ra csökkent, és az Rx ismeretlen. Ha az ellenállásértéken kívül a feszültségek és áramok is ismeretlenek, az Rx ellenállásértéket kétféleképpen számíthatjuk ki:
1. út:
1. először nézzük meg az általános képletet, majd írjuk be az ellenállásértékeket:
![]() ->
-> ![]()
2. 270 és 100 között van egy 2,7-es tényező, csakúgy, mint 330 és az ismeretlen érték között.
330-at 2,7-tel osztva 122,2 Ω ellenállást kapunk.
![]()
2. út:
1. az általános képlet segítségével, amelyben az ellenállásokat keresztezzük:
![]()
2. A képletet úgy alakítjuk át, hogy az = bal oldaláról vesszük Rx-et és elosztjuk R1-gyel. 122,2 Ω ellenállásértéket is elérünk.
![]()
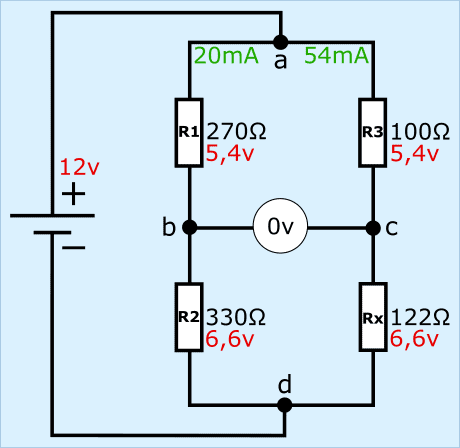
Természetesen ellenőrizzük, hogy van-e kiegyensúlyozott hídunk az előzőleg számított 122 Ω ellenállással.
Az R1 és R2 ellenállások árammal és részfeszültséggel megegyeznek az 1. és 2. bekezdésben szereplő példákkal, tehát ismertnek tekintendők. A híd jobb oldalára koncentrálunk.
1. Számítsa ki az áramerősséget R3-on és Rx-en keresztül:
![]()
2. Számítsa ki a feszültségesést az R3 és Rx ellenállásokon:
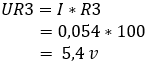
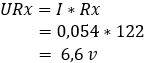
A b és c pontok közötti feszültségkülönbség 0 volt, mivel az R1 és R3 ellenállások egyaránt 5,4-et nyelnek el, így a híd most kiegyensúlyozott.
Kapcsolódó oldalak:
