Driving Resistances:
While driving, the car encounters various resistances:
- Rolling resistance
- Gradient resistance
- Air resistance
- Acceleration resistance
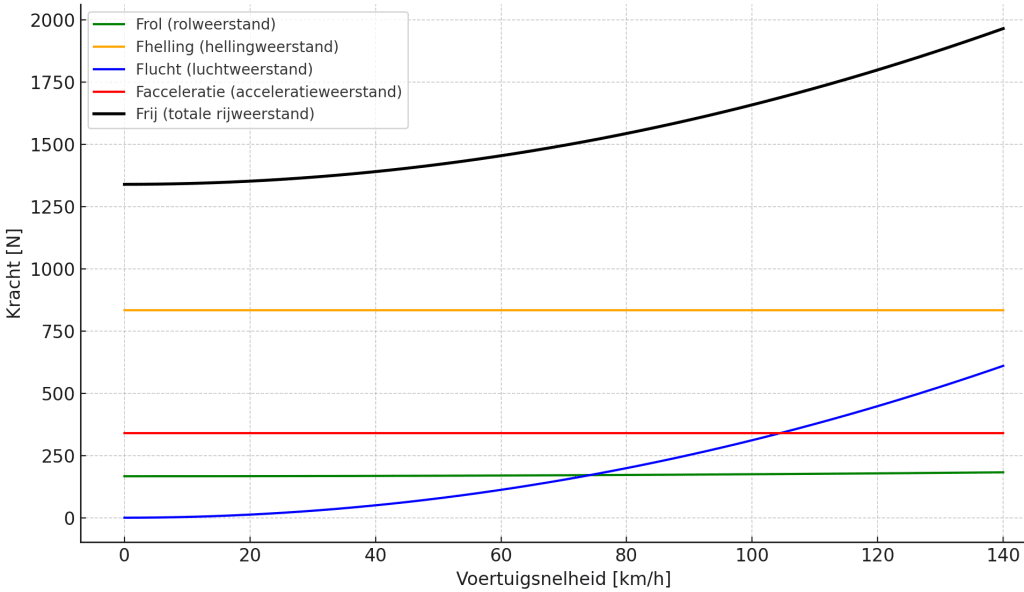
These resistances must be overcome to maintain speed. The power required to do this is called ‘Frij’; it is the sum of all driving resistances.
Rolling resistance increases at higher speeds due to tire deformation, gradient resistance only applies if there is an incline (on a flat road it is 0), and air resistance is very low at low speeds. As driving speed increases, air resistance rises quadratically and plays the largest role in total driving resistances.
This page calculates driving resistances up to the total driving resistance (Frij).
Rolling Resistance:
Rolling resistance arises from various factors such as tire deformation, wheel alignment (and therefore the lateral slip of the tire), and the type of road surface. The extent to which tires deform depends on the tire type. The “smoother” the tire can roll over the road surface (thus encountering minimal resistance), the less force is needed to keep the wheel moving and the lower the fuel consumption will be. On a deformable (soft) surface, such as sand or mud, rolling resistance further increases due to additional frictional forces between the tire and the surface, and the permanent deformation of the surface itself.
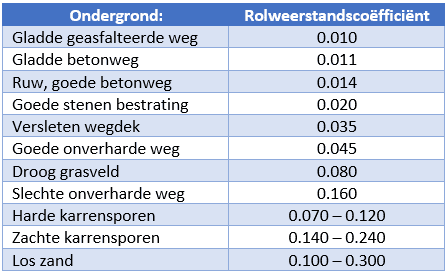
In the adjacent table, we see that the rolling resistance coefficient is low (0.010) on dry asphalt and high (up to 0.3) on sand. The table is based on a low to medium vehicle speed (up to 80 km/h) where the rolling resistance of different types of tires is fairly constant.
At these speeds, the influence of speed on rolling resistance is negligible.
Factors affecting rolling resistance:
- Slip (during braking or accelerating): in the contact patch, slip occurs when the tire transfers forces. With light slip (such as gentle acceleration), rolling resistance may even temporarily decrease. With strong slip (such as hard acceleration or braking), rolling resistance increases due to changes in deformation behavior and more energy loss.
- Wheel alignment (toe-in and camber): incorrect alignment causes extra lateral forces (e.g., with toe-in or camber). These forces increase rolling resistance because the wheel does not roll purely straight but builds up lateral load. The influence becomes stronger with larger deviations in alignment.
- Temperature: As the tire starts rolling, it heats up, changing the rubber’s material properties: damping decreases, stiffness changes, and the tire deforms less. This reduces rolling resistance as temperature rises. The temperature reaches equilibrium after a few minutes, balancing heat production and dissipation.
- Speed: At higher speeds, more deformations occur per second (more revolutions), leading to higher temperatures and greater deformation forces. As a result, rolling resistance increases, especially with tire types with higher hysteresis such as standard or winter tires.
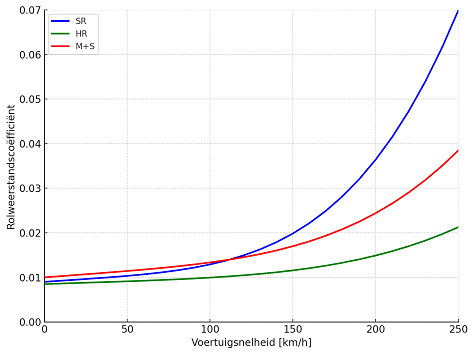
At low speeds (up to about 80 km/h), the rolling resistance coefficient remains largely constant. The table with values for each surface shown at the top of this paragraph assumes these speeds. At higher speeds, rolling resistance increases, especially with standard and winter tires. Mathematically, the increase in rolling resistance can be approximated with a quadratic relation. The chart below illustrates this effect:
- SR tires (standard tires) have relatively high hysteresis and show the strongest increase in rolling resistance at higher speeds.
- M+S tires (winter tires) perform between SR and HR tires. These tires have extra tread and sipes, increasing rolling resistance.
- HR tires (high-performance) have reinforced carcasses and rubber compounds with low hysteresis. They are most efficient at high speed and show the least increase in rolling resistance.
When the rolling resistance coefficient and vehicle weight are known, rolling resistance can be calculated. The following data is known:
- BMW X3 with a mass (m) of 1700 kg;
- Gravitational acceleration (g) is: 9.81 m/s^2;
- Friction coefficient (μ) is: 0.010;
- Horizontal road surface.

First, we multiply the vehicle mass by gravitational acceleration to calculate the normal force (Fn):
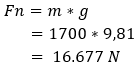
Next, we multiply the normal force by the rolling resistance coefficient to calculate the force required to overcome the rolling resistance of the tires on the road surface.
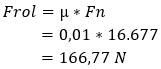
Gradient Resistance:
When a vehicle climbs a gradient, gradient resistance occurs. This resistance arises because part of the vehicle’s weight works against the direction of travel. Additional power from the engine is needed to drive the vehicle upward at a constant speed or acceleration.
When driving uphill, the full weight of the vehicle is no longer exerted perpendicular to the road surface but partly along the gradient. This changes the distribution of forces on the vehicle:
- The part perpendicular to the road surface determines the normal force (Fn), affecting rolling resistance.
- The part parallel to the road surface causes the gradient resistance (Fgradient).
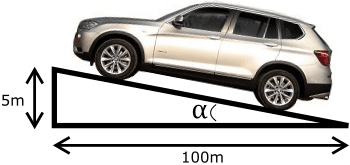
Over a distance of 100 meters, the vehicle has ascended 5 meters (see image). This means the gradient is 5%. We calculate the gradient angle using the tangent (tan).
Calculate tan α:
tan α = opposite / adjacent = 5 / 100
α = tan⁻¹(5/100) = 2.86°
Tip: on the calculator, press shift and then the tan button to get tan ̄ ¹, and put (5/100) in parentheses. The result can be displayed in degrees or radians, depending on your calculator settings. To convert from radians to degrees, use the following formula:
Degrees = Radians * (180 / π)
Rolling resistance decreases slightly when climbing a gradient, because the normal force decreases. A smaller part of the weight acts perpendicular to the road surface, causing the tires to press less firmly on the road, leading to less deformation and thus less rolling resistance.
In the formula for rolling resistance, this is expressed as follows (the cosine of the gradient angle determines how much force still acts perpendicularly):

Its effect on rolling resistance is small, for example only 0.21 N in this case, and is usually neglected in practical situations. We can calculate the gradient force (Fgradient) by multiplying the normal force (Fn) with the gradient angle. The angle is called sine (sin) alpha. The sine of the gradient angle determines how much of the weight acts along the gradient.
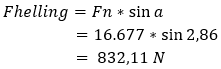
It takes more than 832 Newton + the rolling resistance of 166.56 N to drive up the gradient. We can also combine the formulas of rolling and gradient resistances, as the gradient also affects rolling resistance. Note that air resistance is not yet included, so this is not the total driving resistance yet! This follows further on this page.
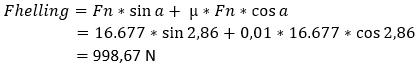
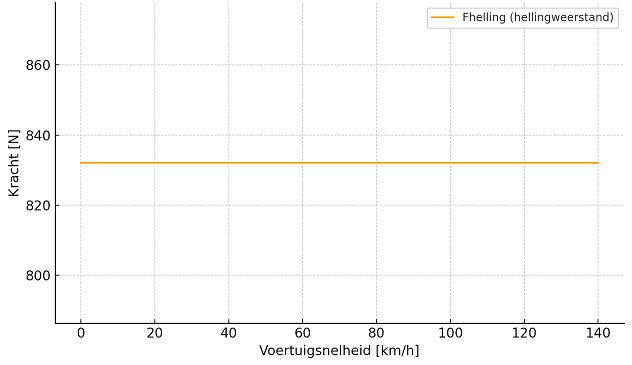
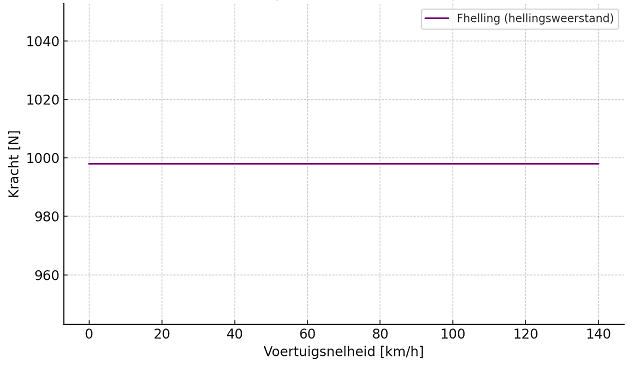
Air Resistance:
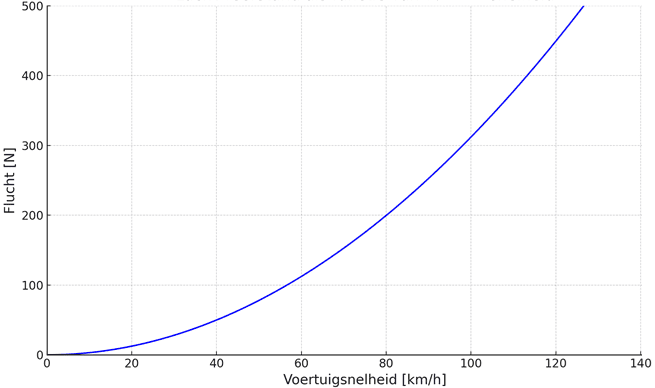
While driving, the vehicle encounters resistance due to headwind, known as air resistance. As speed increases, air resistance rises quadratically. Consequently, the vehicle accelerates less as the speed increases.
When driving on a provincial road, the fuel consumption difference between 60 and 80 km/h is minimal. The consumption difference between 120 and 140 km/h is much greater due to increasing air resistance. At around 90 km/h, consumption is often most favorable due to the ideal engine speed range in the highest gear, see the page on specific fuel consumption.
The power required to overcome air resistance can be calculated as follows:
Explanation of the formula:
½ = one-half, which can be typed on the calculator as 0.5;
ρ = Rho. This represents specific mass, in this case, the specific mass of air, with the unit kg/m³;
Cw = drag coefficient. For a passenger car, the Cw value is between 0.25 and 0.35. For a truck, between 0.65 and 0.75;
A = frontal area of the car (determined in a wind tunnel) in m²;
v² = the vehicle’s speed squared, with the unit m/s.
For this calculation, we use the following data:
- ρ = 1.28 kg/m³ (depending on temperature and humidity)
- Cw = 0.35
- A = 1.8 m²
- v² = 100 km/h = (100 / 3.6) = 27.78 m/s² (meters per second squared as it’s an acceleration):
We fill in the formula for Flucht with the known data:
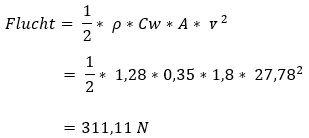
So, a force of 311.11 N is needed to overcome air resistance.
Acceleration Resistance:
During acceleration or deceleration, acceleration resistance arises. Force in Newton is needed to overcome this acceleration resistance. We again consider the BMW X3 with a vehicle mass of 1700 kg.
The force required to overcome acceleration resistance (Facceleration) depends on vehicle mass (m) and acceleration or deceleration force (a) in Newton. In this example, we assume a minimal deceleration of 0.2 m/s². The required force to overcome acceleration resistance can be calculated with the following formula:
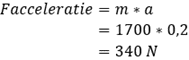
Total Driving Resistance:
The total driving resistances (Frij) are the sum of all previously mentioned resistances. Rolling resistance + gradient resistance + air resistance together form Frij:
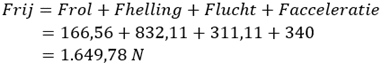
Conclusion: To drive up the 5% gradient at 100 km/h with an acceleration speed of 0.2 m/s² in a windless condition (0 BFT), the total required force amounts to 1,649.78 Newton.
Not only driving resistances but also efficiencies and reductions in the gearbox are important for the constructor to calculate in advance.
The gearbox and gear ratios are tuned to the engine’s characteristics. This is described on the gear ratios page.