Subjects:
- Driving resistances
- rolling resistance
- Slope Resistance
- Air resistance
- Total running resistance
Driving resistances:
While driving, the car encounters various drive resistances:
- rolling resistance
- Slope Resistance
- Air resistance
These resistances must be overcome to maintain speed. We call the power required for this Frij; these are all driving resistances added together.
The rolling resistance is independent of speed (the rolling resistance is about the same at low speeds as at high speeds), the slope resistance only applies if there is a slope (on a flat road it is therefore 0), the air resistance is at low speeds very low. At increasing driving speeds, the air resistance increases quadratically.
On this page, the running resistances are calculated to the total running resistance (Frij).
rolling resistance:
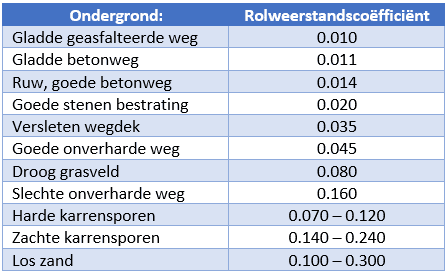
The rolling resistance is caused by various factors such as tire deformation, the lateral running of the tire and the type of road surface. The type of road surface has to do with the driving resistance coefficient. The more “smoothly” the tire can roll over the road surface (i.e. encounters as little resistance as possible), the less force it takes to keep the wheel moving and the lower the Fuel consumption will be.
In the table opposite we see that the rolling resistance coefficient is low (0,010) for dry asphalt and high (up to 0,3) for sand.
When the rolling resistance coefficient and the vehicle weight are known, the rolling resistance can be calculated. The following information is known:
- BMW X3 with a mass (m) of 1700 kg;
- Acceleration (g) is: 9,81 m/s^2;
- Coefficient of friction (μ) is: 0,010;
- Horizontal road surface.

First we multiply the vehicle mass by the acceleration of gravity (gravitational velocity) to calculate the normal force (Fn):
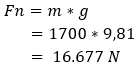
Then we multiply the normal force by the rolling resistance coefficient to get the rolling resistance:
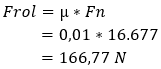
Slope Resistance:
The moment a vehicle drives up a hill, there is a so-called slope resistance. Additional power from the engine is required to accelerate the vehicle. When driving uphill, no force is applied perpendicular to the road surface. So we have to take this into account.
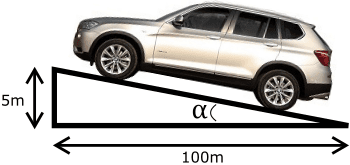
The vehicle has driven up 100 meters over a distance of 5 meters (see picture). That means the slope is 5%. We calculate the angle of inclination with the tanges (tan).
tan α calculate:
tan ̄ ¹ (5/100) = 2,86° (On the calculator, press the shift and then the tan button to get tan ̄ ¹, and don't forget to put 5/100 in parentheses).
The rolling resistance decreases the moment the vehicle goes up a slope. In Frol's formula we multiply the angle of inclination by the normal force and the coefficient of friction. We call the angle cosine (cos) alpha.

The difference in rolling resistance (in this example 0,21 N) is usually neglected.
The ramp force (Fslope) can be calculated by multiplying the normal force (Fn) by the angle of inclination. We call the angle sine (sin) alpha.
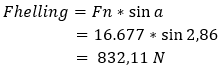
It takes a force of over 832 Newton + the rolling resistance of 166,56 N to drive up the slope. We can also combine the rolling and slope resistance formulas. Please note, the air resistance has not yet been included in this, so this is not yet the total driving resistance!
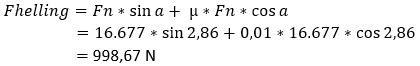
Air resistance:
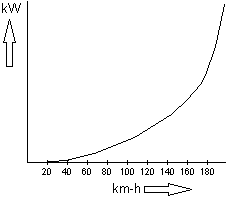
While driving, the vehicle encounters resistance from headwinds. This is called the air resistance. With increasing speed, the air resistance increases squared. For example, the vehicle will accelerate less and less as the vehicle speed increases.
When driving on a provincial road, the difference in fuel consumption between 60 and 80 km/h will be minimal. The difference in consumption between 120 and 140 km/h is a lot bigger due to the increasing air resistance. The consumption is often the most favorable around 90 km/h due to the ideal speed range in the highest gear, see the page about the specific fuel consumption.
The formula to calculate the air resistance looks like this:
Explanation of the formula:
½ = a half, which can be typed into the calculator as 0,5;
ρ = Rho. This indicates the specific gravity. In this case the specific mass of air;
Cw = drag coefficient;
A = frontal area of the car (determined in the wind tunnel);
V² = the speed of the vehicle squared (ie speed x speed);
For this calculation we use the following data:
- ρ = 1,28 kg/m³
- Cw = 0,35
- A = 1,8 m²
- V² = 100 km/h = (100 / 3,6) = 27,78 m/s² (meters per second squared because it is an acceleration):
With the data that are known, we fill in Flucht's formula:

So a force of 311,11 N is needed to overcome the air resistance.
Total running resistance:
The total running resistances (Frij) are all the resistances mentioned above added together. The rolling resistance + the slope resistance + the air resistance together becomes Frij:

To drive on the 5% slope at 100km/h with a constant speed when there is no wind (0 BFT), a force of 1.309,78 Newtons is needed at the wheels.
Not only the driving resistance, but also the yields and the reductions in the gearbox are important for the manufacturer to calculate in advance.
The gearbox and gear ratios are matched to the characteristics of the engine. This is described on the page gear ratios.
