Subjects:
- Gear ratios introduction
- Power at the wheels
- Determining K-factor according to the geometric series
- Determining the K-factor according to the corrected geometric series (Jante's series)
- Determining gear ratios (introduction)
- Calculate 1st gear reduction
- Calculating the reduction of the 5th gear (according to the geometric series)
- Calculating other reductions (according to the geometric series)
- Calculating reductions according to the corrected geometric series (Jante series)
- Calculate vehicle speed per reduction (geometric series)
- Calculate vehicle speed per reduction (corrected geometric series)
Gear ratios introduction:
The gear ratio is determined by:
- The number of teeth of the gears (such as the gearbox)
- The diameter of the pulleys (such as the components driven by the V-ribbed belt)
The picture shows that gear A has 20 teeth and gear B has 40 teeth. The ratio is 40/20 = 2:1.
That means gear A (driven) makes two revolutions when gear B makes one revolution. In practice this is never the case. A ratio is always ensured that is never exactly 2,00:1, because in the latter case the same teeth mesh with each revolution. If gear B had 39 teeth (1,95:1) or 41 teeth (2,05:1) the gears of A and B mesh one tooth further each revolution, so that the wear is 20 times less than the ratio from 2:1.
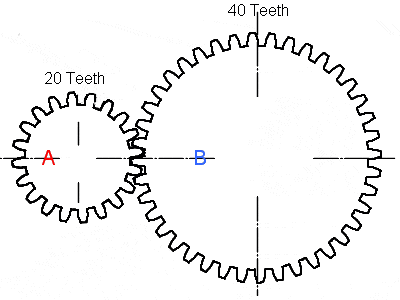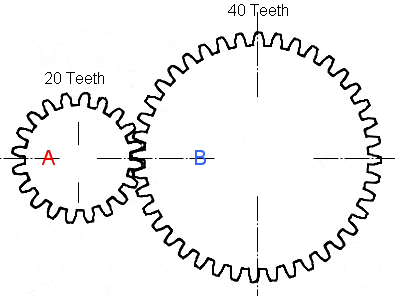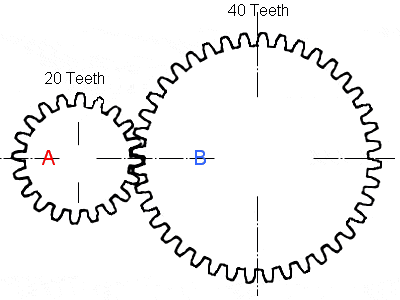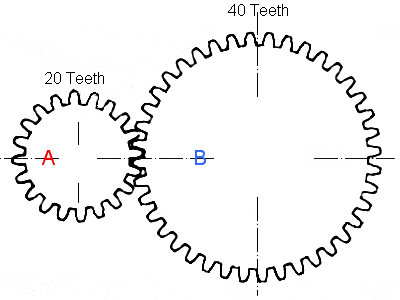
A high gear ratio (where the driving gear is small and the driven gear is large) gives a high top speed and a low gear ratio gives more pulling power. In the gearbox of a car (in principle all motor vehicles) the purposes for which the car will be used are taken into account in the design. A car that is primarily intended to carry a heavy load will require more pulling power at low gears than a sports car that must be able to reach a high top speed. The transmission ratio of the highest gear must be constructed in such a way that the maximum engine speed can be achieved at the maximum engine power. It would be a shame if the speed is already at the limit and there is still enough power surplus to be able to accelerate further. In addition to the highest gear, the lowest gear must also be chosen carefully; the car must be able to pull away without any problems in first gear on a 40% gradient in the worst conditions. In addition, the ratios of the intermediate gears, so 2, 3 and 4 (possibly also 5 if it concerns a 6-speed) between them must be determined.
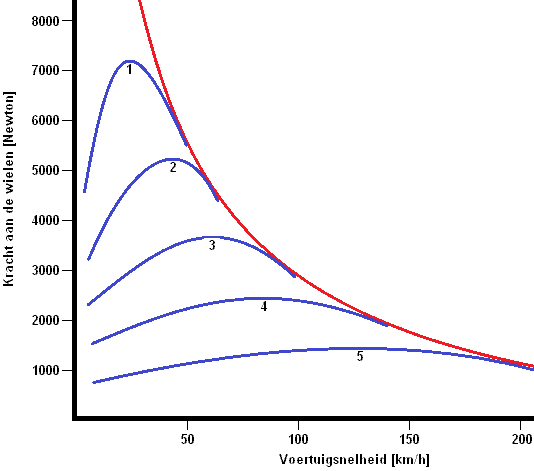
Power at the wheels
In the graph (in the picture) the engine characteristic is indicated by the blue lines and the vehicle characteristic by the red line. Here you can clearly see that the 1st gear delivers a high force to the wheels (about 7200N, so 7,2kN) and with the highest gear (the 5th) a force of up to 1500N delivers to the wheels.
As vehicle speed and accelerations increase, the power delivered to the wheels decreases. The course of the blue lines is a result of the transmission ratios and the descending red line is the result of the driving resistance (rolling and air resistance).
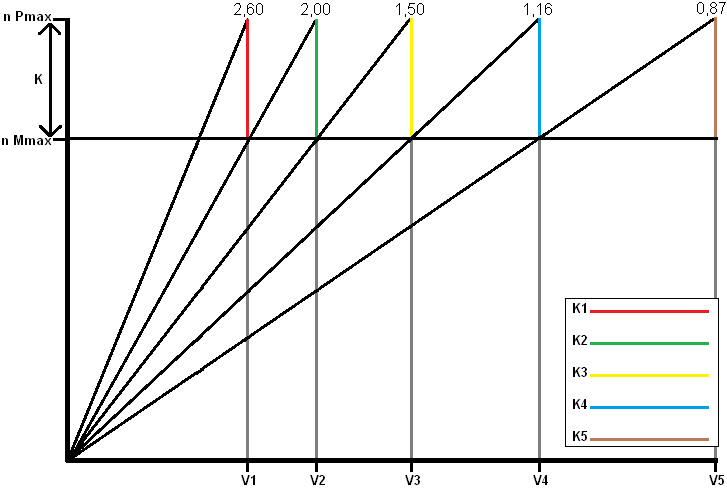
Determining K-factor according to the geometric series:
The following text refers to the sawtooth diagram below.
When accelerating in 2st gear to maximum engine speed, it is necessary to shift to XNUMXnd gear.
After shifting and disengaging, the engine speed will have dropped and the vehicle speed will still be the same. When shifting from 1st to 2nd gear, the engine speed follows the red line in the graph below. The engine speed will drop from “n Pmax” to “n Mmax”.
The colored lines outline the K-factor. The size of the K-factor determines the size of the colored lines. If “n Mmax” and “n Pmax” are close to each other, the K factor is small. So there are smaller gaps between the transmissions.
The same goes for the other gears. When accelerating to “n Pmax” of 2nd gear (up to V2), the green line is followed to “n Mmax” when shifting.
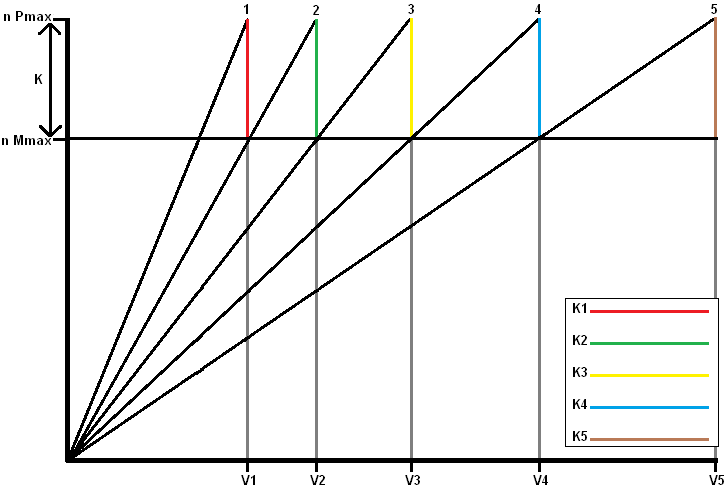
- n Pmax: The engine speed at which maximum power is achieved (e.g. 6000 rpm) with “n Pmax” as “speed at maximum power”
- n Mmax: The engine speed at which maximum torque is achieved (e.g. 4000 rpm) with “n Mmax” as “speed at maximum torque”
The ratios between the speeds and the gears remain the same. All colored lines (K1 to K5) therefore remain the same. The K-factor is determined by the motor characteristic. The K-factor is between the engine speeds of maximum torque and maximum engine power. The transmissions of the gearbox are therefore calculated on this engine characteristic. The K-factor for the geometric series can be determined as follows:
K = nPmax / nMmax
K = 6000 / 4000
K = 1,5
The K-factor of 1,5 determines the reductions (transmissions) of all gears. These are all coordinated in this way. The geometric series is not applied to passenger cars because of the oversized holes in the higher gears. The gearboxes of passenger cars are designed according to the corrected geometric series (Jante series).
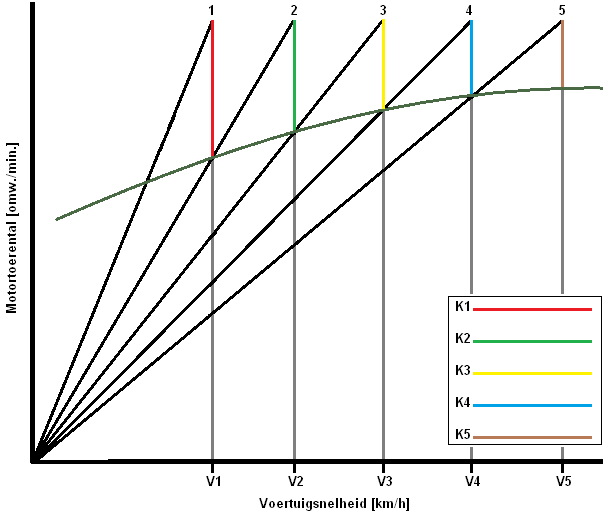
Determining the K-factor according to the corrected geometric series (Jante's series):
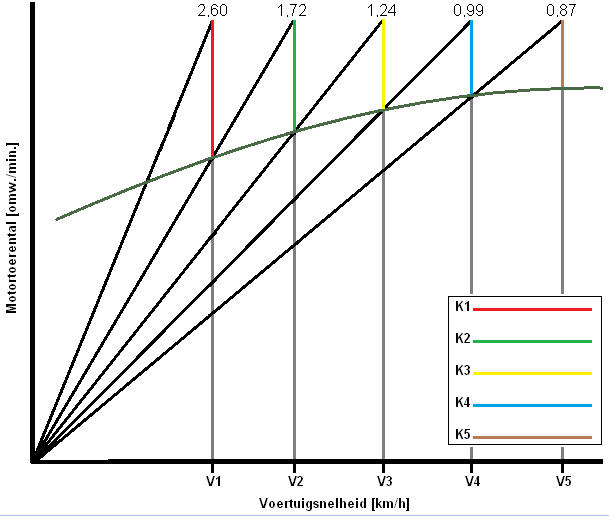
In passenger cars, the gaps between the low gears are often large and become smaller and smaller in the higher gears. Small gaps between the high gears give little acceleration loss. The ratios in the higher gears become smaller and smaller, so that the engine power is used to the maximum. You can also notice this; the engine speed drops further between shifting from 1st to 2nd gear than between shifting from 3rd to 4th gear. This is visible in the sawtooth diagram below; the red line is larger than the yellow line:
The arithmetic series is also called “Jante's series”. It is a corrected geometric series.
The K-factor is different between all gears. This has great advantages compared to the aforementioned geometric series with the fixed K-value. Because the ratios in the higher gears become smaller and smaller, the engine power is used to the maximum. The force on the wheels is now greater than with the geometric series.
The K-factor is now different for each gear (all colored lines have a different length), so it must now all be determined with a calculation. The transmission ratios of the gears can be determined using the K-factor. Without the K factor being known, the reduction of the lowest or highest gear can be determined, but the rest of the gears must then be calculated with the K factor. Only then can the sawtooth diagram be drawn.
Determining gear ratios (introduction):
The gearbox manufacturer has to take a number of things into account. The transmissions in the gearbox must be assembled with care. Factors such as the speeds where the engine has the most torque and power, the dynamic tire radius, the reduction of the differential and the efficiency of the total drivetrain are important. This is listed below:
The RPMs where the engine has the most torque and power:
These are the speeds “n Pmax” and “n Mmax” shown in the geometric series image above.
The dynamic tire radius:
This is the distance between the center of the hub and the road surface. The smaller the wheel, the higher the speed of the wheel will be at the same vehicle speed. The dynamic band radius can be calculated as follows (if already known):
The tire size must be known to calculate this. Let's take the tire size 205/55R16 as an example. That means that the tire (205 x 0,55) = 112,75mm = 11,28cm high. Since it is 16 inches, this must be converted to centimeters: 16 x 2,54(inch) = 40,64cm.
It concerns the distance between the road surface and the hub, so the total height of 40,64 cm still has to be divided by 2: 40,64 / 2 = 20,32 cm.
The dynamic tire radius (Rdyn) is now: 11,28 + 20,32 = 31,60cm.
The reduction of the differential:
The differential always has a fixed gear ratio. The gearbox must be geared to that. Commercial vehicles can have up to 5 differentials in the drive.
The efficiency of the total powertrain:
Due to friction losses, among other things, there is always a certain percentage loss. This also depends on the thickness of the oil (and the temperature). Usually the return is around 85 to 90%.
Now we are going to determine the transmission ratios (reductions) of a fictitious engine and gearbox.
The following specifications are known:
- Vehicle mass: 1500kg
- Acceleration (G): 9,81m/s2
- Gearbox type: 5-speed manual gearbox and one reverse
- Dynamic tire radius: 0,32m (= 31,60cm from the previous calculation)
- Reduction of the differential: 3,8:1
- Drivetrain efficiency: 90%
- Maximum vehicle speed: 220km/h (220 / 3,6 = 61,1m/s)
- Maximum slope: 20%
- Rolling resistance coefficient (μ): 0,020
- n Pmax: 100kW at 6500 rpm
- n Mmax: 180Nm at 4500 rpm

First, it must be determined how much torque the wheels can transfer to the road surface. This depends on the condition of the vehicle, because is it driving on an asphalt road with a low rolling resistance coefficient? This can be calculated together with the rolling resistance and the dynamic tire radius. The formula for rolling resistance is as follows:
Frol = μ xmxgx cos α (for explanation, see the page driving resistances)
Frol = 0,020 x 1500 x 9,81 x cos 18 = 279,9 N
Since there is a slope, Fslope must also be calculated:
Fslope = mxgx sin
Fslope = 1500 x 9,81 x sin 18 = 4547,2 N
The air resistance can be neglected, so the total driving resistance is as follows:
Frij = Frol + Fslope
Frij = 279,9 + 4547,2 = 4827,1N
To calculate the maximum torque that the wheels can transfer to the road surface, the Frij must be multiplied by the dynamic tire radius.
Mwiel = Free x Rdyn
Mwheel = 4827,1 x 0,32
Mwheel = 1544,7Nm
K factor:
Now we are going to calculate the K-factor:
K = nPmax / nMmax
K = 6000 / 4500
K = 1,33
Calculate 1st gear reduction:
The formula of calculating the first gear is as follows:
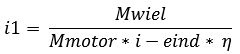
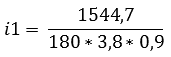
Calculating the reduction of the 5th gear (according to the geometric series):
The reduction of the 5th gear can also be determined in a similar way. The 5th gear should be determined on the basis of the maximum engine speed, because it would be annoying if the engine still has enough power to accelerate further while the maximum engine speed (and therefore the top speed of the car) has been reached. The speed of the wheel (nWheel) at the maximum vehicle speed is also important. This must first be calculated:
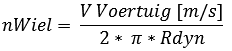
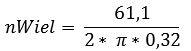
Now that the speed of the wheel is known at the maximum vehicle speed of 220 km/h (61,1 meters per second), the reduction of the 5th gear can be calculated.
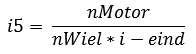
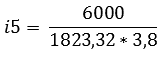
To calculate other reductions (according to the geometric series):
According to the calculations, the reduction of the 5th gear is 0,87 and the K factor = 1,33.
With this data (according to the geometric series) the reductions of the 2nd, 3rd and 4th gears can be calculated.
i5 = (has already been calculated before)
i4 = K × i5
i3 = K × i4
i2 = K × i3
i1 = K × i2
The reduction i1 is already known here, so if the remainder is calculated correctly, it should result in the same number (namely 2,51). A small deviation is normal, because many roundings have been made in the meantime. Now the row of all reductions can be filled in. It must be calculated from top to bottom. The answer of i5 is used with i4, and of i4 with i3 etc.
i5 = 0,87
i4 = 1,33 x 0,87 = 1,16
i3 = 1,33 x 1,16 = 1,50
i2 = 1,33 x 1,50 = 2,00
i1 = 1,33 x 2,00 = 2,60
The table of the geometric series can now be filled in.
Calculating reductions according to the corrected geometric series (Jante series):
Earlier on the page, the difference between the geometric series and the “corrected” geometric series was explained. The corrected geometric series, also called the "Jante series", has the advantage that the K-factors are closer together at the higher reductions. The K factor in the geometric series was constant (this was n P max divided by n M max, and was 1,33). This also gave a constant value in the graph.
In the corrected geometric series, a line runs in the graph that indicates that the K value is not constant. With each acceleration, the K-factor gets smaller.
The corrected geometric series does have a constant value. We indicate this with an m. The value of m = 1,1.
The general formula of the K-value of the corrected geometric series is as follows:

Explanation of the formula:
z-1 = the number of gears minus one
i1 = first gear reduction
m to the sixth power = constant to the 6th
iz = the total number of gears
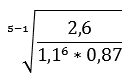
Filled in, this gives the square root of 2,6 / (1,1^6 x 0,87)
(Type the quadratic root into the calculator as follows: first press 4, then SHIFT followed by the radical sign with an x above it. Then put the multiplication below the division bar in parentheses).
The answer will be: 1,14
The K-value of the corrected geometric series is therefore 1,14. We will continue to calculate with this:
i5 = (previously calculated)
i4 = K × i5
i3 = K2 xmx i5
i2 = K3 x m3 x i5
i1 = K4 x m6 x i5
i5 is known; this is 0,87. The K value is 1,14 and m is 1,1. With this data we can fill in the table:
i5 = 0,87
i4 = 1,14 x 0,87
i3 = 1,142 x 1,1 x i5
i2 = 1,143 x 1,13 x i5
i1 = 1,144 x 1,16 x i5
i5 = 0,87
i4 = 0,99
i3 = 1,24
i2 = 1,72
i1 = 2,60
The table of the corrected geometric series can now be filled in:
Calculate vehicle speed per reduction (geometric series):
The vehicle speed can be determined for each reduction. This is the maximum speed that the vehicle can achieve in this gear at the maximum speed of 6000 revolutions per minute. The calculation is as follows:
Vvehicle 1st reduction = 2 x π x nWheel x Rdyn
(nWheel has just been calculated for the first gear and Rdyn was already known; this is 0,32m. The formula can then be filled in:
Vvehicle 1st reduction = 2 x π x 10,12 x 0,32
Vvehicle 1st reduction = 20,35 m/sx 3,6 = 73,25 km/h
The other accelerations can be calculated simply by changing the Z = 2,60 in the first formula to the reduction of the desired acceleration, and then filling it in as nWheel in the second formula.
The other gears have the following outcome:
2nd gear: 95,2 km/h
3nd gear: 127 km/h
4nd gear: 164,2 km/h
5nd gear: 219 km/h (this is the top speed of the car)
These velocities can be entered in the table of the geometric series.
Calculate vehicle speed per reduction (corrected geometric series):
The calculation is exactly the same and is therefore no longer noted.
1st gear: 73,2 km/h
2st gear: 110,75 km/h
3st gear: 153,61 km/h
4st gear: 192,40 km/h
5st gear: 219 km/h
As can now be clearly seen, the top speeds of the car are the same for the geometric and the corrected geometric series. In the geometric series (the first) the gaps between the higher gears are very large and in the corrected geometric series the gaps between all the gears are almost equal. The latter is used in today's vehicles.
