denekler:
- Virajda ayak parmağının dışarı çıkması
- Gönderilen açıların hesaplanması
Virajda ayak parmağının dışarı çıkması:
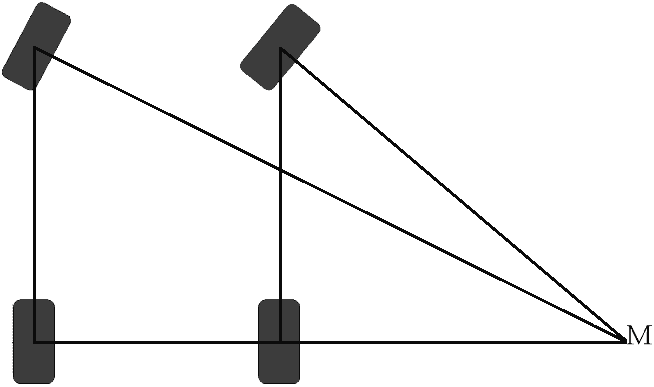
Viraj alırken ön tekerlekler aynı açıda yönlenmiyor. İç tekerlek her zaman dış tekerleğe göre “daha keskin” bir dönüş yapacaktır. Resim bunun neden böyle olduğunu gösteriyor.
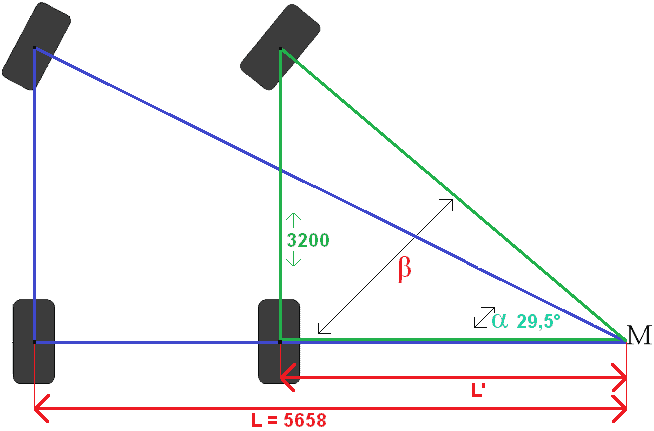
Resimde ön tekerleklerden gelen çizgilerin M açısında bittiği gösterilmektedir. M açısı her iki ön tekerleğin ortak dönme noktasıdır. Eğer tekerlekler aynı açıda dönseydi (tekerleklerin her ikisi de tam olarak aynı konumda olsaydı), tekerleklerden gelen çizgiler de birbirine sonsuza kadar paralel uzanırdı. Hiçbir zaman ortak pivot noktası M'yi bulamazlar. Dolayısıyla bu durumda direksiyon özellikleri çok zayıf olacaktır. Bütün bu prensibe "virajda parmak ucu" denir. Tüm modern arabalar bu özellik ile üretilmiştir.
Pürüzsüz yüzeylerde, örneğin otoparkın zemininde, dönüş sırasında lastiklerin gıcırdaması duyulabilir. İşte bu prensipten dolayı. Dışa göre daha keskin bir açıya sahip olan iç tekerlek bir miktar kayma yaşayacaktır. Buna direksiyon hatası denir. Direksiyon hatasıyla ilgili daha fazla bilgiyi (ve bir grafiği) sayfada bulabilirsiniz. direksiyon hatası.
Bu sayfada her iki ön tekerleğin giriş açılarının (derece cinsinden) bir dizi veri kullanılarak nasıl hesaplanabileceği açıklanmaktadır.
Gönderilen açıların hesaplanması:
Girilen açıların hesaplanması için aşağıdaki araç verileri gereklidir:
- Parça genişliği
- wielbase
- Dönme dairesi çapı
- Direksiyon mafsalı mesafesi (bu sayfada direksiyon mafsalı mesafesini iz genişliğine eşit tutuyoruz)
- Lastik ebadı (hesaplamaya bağlıdır. Bu sayfada hesaplamalar için lastik ebadı kullanılır, ancak tampon köşelerine kadar da hesaplama yapılabilir. Ancak daha fazla köşe eklenecektir).
| Parça genişliği = 1600mm | Dingil mesafesi = 3200mm |
| Dönme dairesi çapı = 13,225m | Mafsal aralığı = İz genişliği = 1600 mm |
| Lastik ebadı = 225 | L ve L' = bilinmiyor |
Sembollerin açıklaması:
α = Alfa
β = Beta
γ = Gama
Bu harfler Yunan alfabesindendir ve sıklıkla açı hesaplamalarında kullanılır.
L = uzunluk
L' = L, ek olarak "vurgu" ile birlikte, genellikle matematiksel olarak kullanılır. L2 de diyebiliriz. Örneğin, 3. L'nin iki aksanı vardı: L".
Aynı şey R için de geçerlidir”.
Alfa, Beta ve Gama açıları M noktasındadır.
Alfa Açısı + Gama = Beta açısı.
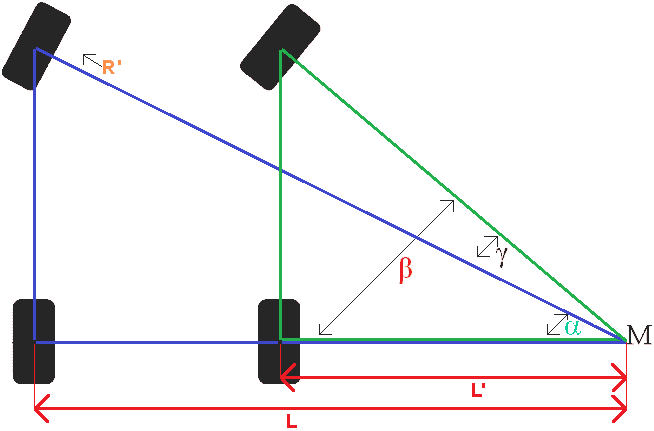
Dönüş çapının tamamı 13,225 metredir. R yarıçaptır, dolayısıyla yarım dönüş dairesi (6612,5) olur. Şekilde R' verilmiştir. Bu R' sabit bir gerçek değildir. Bu, bant genişliğinin yarısının çıkarılmasıyla hesaplanmalıdır. Başka bir yol da direksiyon mafsalı mesafesini çıkarmaktır, ancak bu sayfada şunu kullanıyoruz: İz genişliği = direksiyon mafsalı mesafesi. Basit hesaplama şu şekildedir:
R = 6612,5 mm
R' = R – yarım bant genişliği
R' = 6612,5 – (225 : 2)
R' = 6612,5 – 112,5
R' = 6500 mm
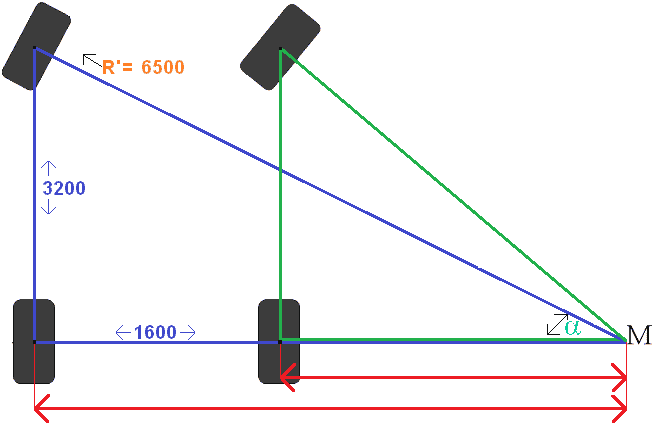
Resimdeki R' harfini dolduruyoruz. Daha sonra Sinüs Kuralını kullanarak sin α (sinüs Alfa) açısını hesaplarız. Daha sonra Teğet ve Pisagor Teoremini kullanarak kalan açıları hesaplıyoruz.
Sinüs ile açı hesabı:
Sin α = Karşı taraf: Eğik taraf
Sin α = Wb : R'
Sin α = 3200 : 6500
Günah α = 0.492
Inv Sin α = 29,5°
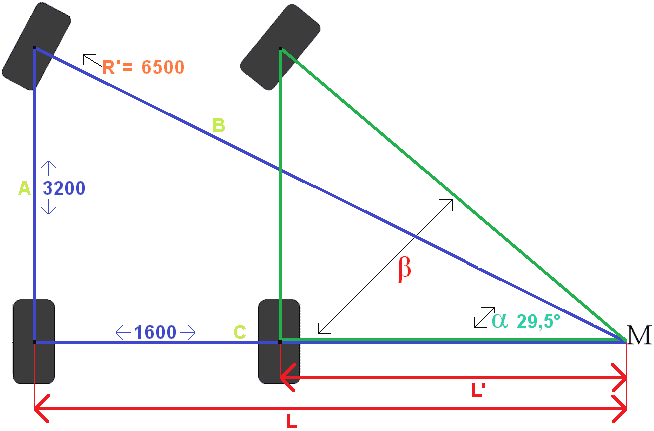
Hesaplamanın açıklaması:
Sin α'yı hesaplamak istiyoruz. Sinüs karşı tarafta eğik tarafla bölünür (anımsatıcı: SIN = SOS).
Wb= dingil mesafesi = 3200 mm. Daha önce R' = 6500 mm'yi hesaplamıştık.
Daha sonra bunu birlikte paylaştırıyoruz; o zaman Sin α = 0.492 elde ederiz. Daha sonra bu sayıyı bir açıya dönüştürmek için hesap makinesine sin-1 düğmesini girin (genellikle önce Shift düğmesine ve ardından Sin tuşuna basın), ardından 0.492'yi veya ANS düğmesini girin. Artık 29,5 derecelik açı ortaya çıkıyor.
Sin α artık biliniyor. Şimdi aslında tan β'yı hesaplamak istiyoruz, ancak o zaman L' uzunluğuna ihtiyacımız var. Öncelikle bunun hesaplanması gerekiyor. Bu nedenle L' hesaplamasının cevabını daha sonra Tan β'yı hesaplamak için kullanırız.
L' = L – İz genişliği.
L'yi Pisagor teoremini kullanarak hesaplıyoruz. Üçgenin 2 tarafı bilinmektedir (6500 ve 3200). 1600'ün diğer tarafı lastikten lastiğe uzanan iz genişliğidir, dolayısıyla sayılmaz. Sol arka lastikten M ortak noktasına kadar uzanan alt tarafı hesaplayacağız. Bu nedenle hesaplama mavi üçgenin tamamıyla ilgilidir.
Pisagor teoremi şuna benzer:
A^2 + B^2 = C^2. (^ işareti “güç” sembolüdür. Yani A kare + B kare = C kare diyor. Burada biraz farklı formüle ediyoruz.
Uzunluğuna 3200 A, 6500 uzunluğuna B dediğimiz ve en alttaki bilinmeyen tarafa C diyoruz:
C^2 = 6500^2 – 3200^2
C^2 = 42250000 – 10240000
C^2 = 32010000^2
Kareyi yok etmek için sayının karekökünü alırız.
C^2 = √32010000
C = 5658 mm.
C tarafı aslında L uzunluğudur.
Artık L' hesaplanabilir. Tam uzunluk L ve iz genişliği bilindiğinden ikisi birbirinden kolayca çıkarılabilir:
L' = L – İz genişliği
L' = 5658 – 1600
U' = 4058 mm
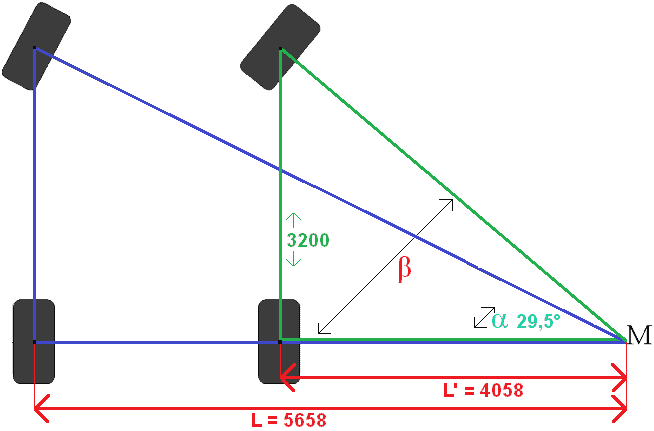
Artık Wb ve L' bilinmektedir. Üçgenin üç kenarından ikisi biliniyor, dolayısıyla üçüncü kenarı bulmak için Teğet'i kullanabilirsiniz. Worden hesaplandı:
Teğet ile açı hesabı:
Tan β = Karşı taraf : Bitişik taraf
Tan β = Wb : L'
Tan β = 3200 : 4058
Tan β = 0.789
Ters Tan β = 38,3°
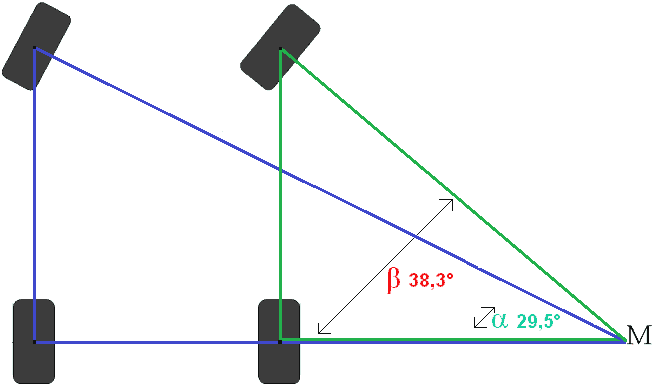
Hesaplamanın açıklaması:
Tan β'yı hesaplamak istiyoruz. Teğet, karşı tarafı bitişik kenara bölüyor (anımsatıcı: TAN = TOA).
Wb= dingil mesafesi = 3200 mm. Daha önce L' = 4058 mm'yi hesaplamıştık.
Daha sonra bunu birlikte paylaştırıyoruz; o zaman Tan β = 0.789 elde ederiz. Daha sonra bu sayıyı bir açıya dönüştürmek için hesap makinesine tan-1 düğmesini girin (genellikle önce Shift düğmesine ve ardından Tan tuşuna basın), ardından 0.789'u veya ANS düğmesini girin. Artık 38,3 derecelik açı ortaya çıkıyor.
Artık her iki ön tekerleğin direksiyon açıları hesaplandı. Sol ön tekerlek 29,5°, sağ ön tekerlek ise 38,3° açıdadır. Bu, direksiyon açısının her iki tekerlekte de 8,8°'lik bir farka sahip olduğu anlamına gelir. Sola virajda aynı direksiyon açısı aynı direksiyon açısıyla sonuçlanacaktır.
Sayfa işlemi tekerlek geometrisi çeşitli tekerlek konumları açıklanmıştır.
