Soggetti:
- Introduzione
- Ponte di Wheatstone in equilibrio
- Ponte sbilanciato di Wheatstone (valori di resistenza noti)
- Ponte di Wheatstone con valore di resistenza sconosciuto
Introduzione:
Il ponte di Wheatstone è un circuito a ponte elettrico per misurare con precisione la resistenza elettrica costante o variabile. Questo circuito può essere utilizzato per misurare grandezze fisiche come temperatura e pressione, come vediamo nel misuratore della massa d'aria (temperatura del filo caldo) e Sensore MAP (pressione nel collettore di aspirazione).
Ce ne sono quattro sul ponte di Wheatstone resistori, tre dei quali hanno una resistenza nota e uno ha una resistenza sconosciuta. Il ponte è in realtà costituito da due partitori di tensione collegati in parallelo.
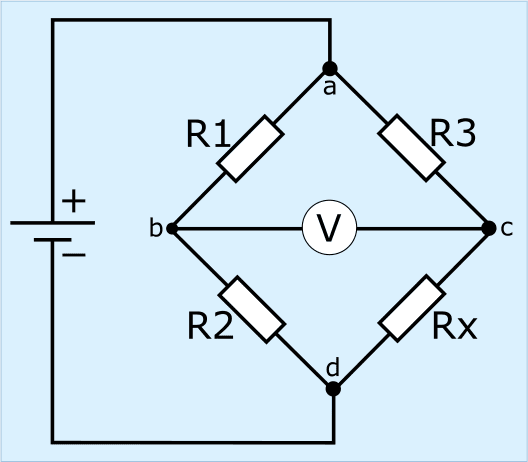
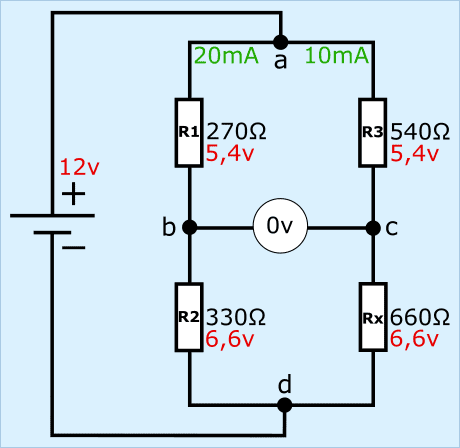
Nell'immagine vediamo i resistori da R1 a R3 (valori di resistenza noti) e Rx (sconosciuto), con un voltmetro al centro dei due partitori di tensione e una sorgente di tensione a sinistra del ponte.
Il ponte di Wheatstone è bilanciato quando la tensione di uscita tra i punti b e c è pari a 0 volt. Nei paragrafi successivi vengono illustrate diverse situazioni.
Ponte di Wheatstone in equilibrio:
Il ponte di Wheatstone è bilanciato o equilibrato quando la tensione di uscita è pari a 0 volt, perché i valori di resistenza a sinistra e a destra sono proporzionati tra loro.
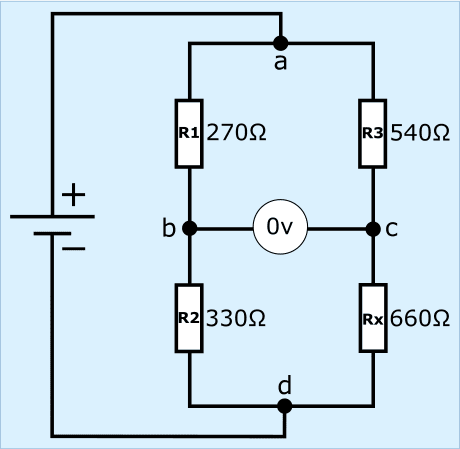
Il circuito in questa sezione è disegnato diversamente rispetto alla sezione precedente, ma si basa sulla stessa operazione.
- i resistori R1 e R2 hanno una resistenza di 270 e 330 Ω. Sommati insieme si ottengono 600 Ω;
- i resistori R3 e Rx hanno una resistenza di 540 e 660 Ω. Sommati insieme si ottengono 1200 Ω.
I rapporti tra i resistori a sinistra e a destra sono gli stessi. Ciò significa che i rapporti di resistenza e le cadute di tensione sono uguali tra R1 e R3, nonché tra R2 e Rx.
Le formule seguenti mostrano i rapporti di resistenza uguali e le cadute di tensione:
![]() en
en ![]()
Con una tensione di alimentazione e valori di resistenza noti, possiamo determinare le cadute di tensione attraverso i resistori e quindi la differenza di tensione tra i punti b e c. Nell'esempio seguente calcoliamo la differenza di tensione tra i punti b e c per un ponte di Wheatstone bilanciato. La conoscenza del Legge di Ohm e calcola con circuiti in serie e in parallelo è un requisito.
1. calcolare le correnti attraverso i resistori R1 e R2 (RV = resistenza di sostituzione):
![]()
2. calcolare la caduta di tensione sui resistori R1 e R2:
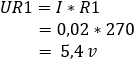
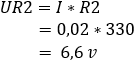
3. calcolare le correnti attraverso i resistori R1 e R2:![]()
4. calcolare la caduta di tensione sui resistori R3 e Rx:
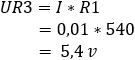
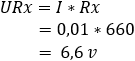
La tensione nei punti b e c è di 5,4 volt. La differenza di potenziale è pari a 0 volt.
Ponte sbilanciato di Wheatstone (valori di resistenza noti):
Come risultato di una variazione della resistenza di Rx, il ponte di Wheatstone risulterà sbilanciato. La variazione della resistenza può verificarsi a causa, ad esempio, di una variazione della temperatura, dove Rx è a termistore È. Il partitore di tensione tra R1 e R2 rimarrà lo stesso, ma non tra R3 e Rx. Poiché in quel punto il partitore di tensione cambia, otteniamo una tensione diversa nel punto c. In questo esempio, il valore della resistenza di Rx è sceso da 600 Ω a 460 Ω.
1. calcolare le correnti attraverso i resistori R1 e R2:
![]()
2. calcolare la caduta di tensione sui resistori R1 e R2:
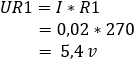
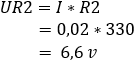
4. calcolare la caduta di tensione sui resistori R3 e Rx:
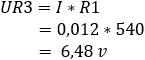
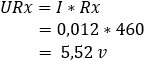
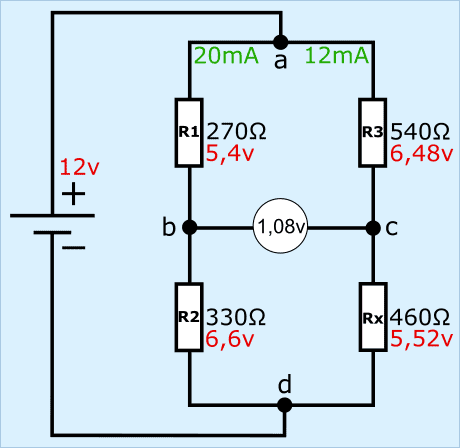
Nei due esempi, il valore della resistenza di Rx è cambiato da 660 Ω a 460 Ω. Questo cambiamento di resistenza ha fatto sì che la tensione tra bc cambiasse da 0 volt a 1,08 volt. Se questo ponte di Wheatstone è integrato nell'elettronica del sensore, la tensione di 1,08 volt viene considerata come tensione di segnale. Questa tensione di segnale viene inviata all'ECU tramite un cavo di segnale. IL Convertitore A/D nella ECU converte la tensione analogica in un messaggio digitale, che può essere letto dal microprocessore.
Ponte di Wheatstone con valore di resistenza sconosciuto:
Nelle sezioni precedenti abbiamo assunto un valore di resistenza noto di Rx. Poiché questo valore di resistenza è variabile, possiamo fare un ulteriore passo avanti e calcolare questo valore di resistenza per bilanciare il ponte di Wheatstone.
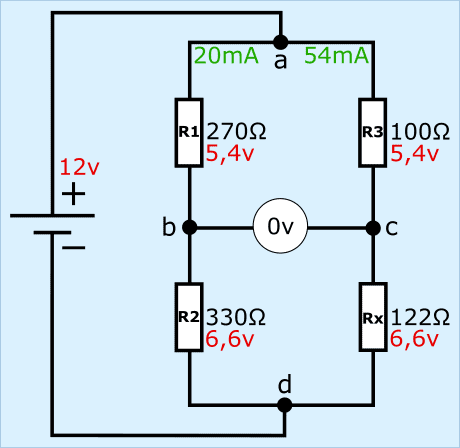
In questo circuito R1 e R2 sono ancora 270 e 330 Ω. La resistenza di R3 è stata ridotta a 100 Ω e Rx è sconosciuta. Se oltre al valore della resistenza non si conoscono anche le tensioni e le correnti, possiamo calcolare il valore della resistenza Rx in due modi:
Modo 1:
1. guardiamo prima la formula generale e poi inseriamo i valori di resistenza:
![]() ->
-> ![]()
2. Tra 270 e 100 c'è un fattore di 2,7, così come tra 330 e il valore sconosciuto.
Dividendo 330 per 2,7 arriviamo ad una resistenza di 122,2 Ω.
![]()
Modo 2:
1. tramite la formula generale in cui moltiplichiamo in modo incrociato le resistenze:
![]()
2. convertiamo la formula prendendo Rx dal lato sinistro di = e dividendo per R1. Arriviamo anche ad un valore di resistenza di 122,2 Ω.
![]()
Naturalmente controlliamo se abbiamo un ponte bilanciato con la resistenza precedentemente calcolata di 122 Ω.
I resistori R1 e R2 con le correnti e le tensioni parziali sono gli stessi degli esempi dei paragrafi 1 e 2, quindi si considerano noti. Ci concentriamo sul lato destro del ponte.
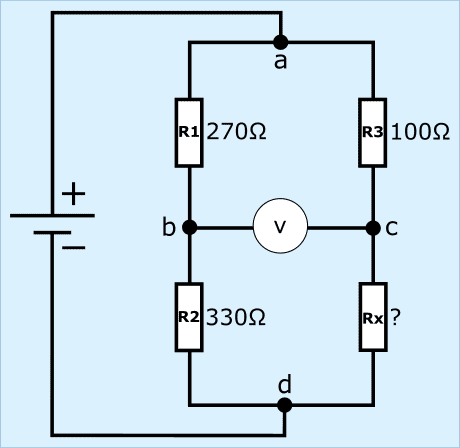
1. calcolare la corrente attraverso R3 e Rx:
![]()
2. calcolare la caduta di tensione sui resistori R3 e Rx:
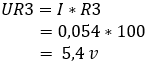
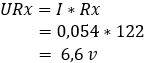
La differenza di tensione tra i punti b e c è 0 volt perché i resistori R1 e R3 assorbono entrambi 5,4, quindi il ponte ora è bilanciato.
Pagine correlate:
