Tárgyak:
- Kihajlás a kanyarban
- A leadott szögek kiszámítása
Kihajlás a kanyarban:
Az első kerekek nem ugyanabban a szögben kormányoznak kanyarban. A belső kerék mindig „élesebben” fordul, mint a külső kerék. A képen látható, hogy miért van ez így.
A képen látható, hogy az első kerekek vonalai az M szögben végződnek. Az M szög mindkét első kerék közös forgáspontja. Ha a kerekek azonos szögben forognának (mindkettő pontosan ugyanabban a helyzetben van), a kerekek vonalai is párhuzamosan futnának egymással a végtelenségig. Soha nem találják meg a közös M forgáspontot. Ezért a kormányzási jellemzők ebben a helyzetben nagyon rosszak lesznek. Ezt az egész elvet „kanyarban kihajlásnak” nevezik. Minden modern autót ezzel a funkcióval gyártanak.
Sima felületeken, például a parkolóházban a padlón kanyarodáskor a gumik csikorgása hallható. Ez ennek az elvnek köszönhető. A belső kerék, amely élesebb szöget zár be, mint a külső, bizonyos mértékű csúszást tapasztal. Ezt kormányhibának hívják. A kormányhibáról további információ (és egy grafikon) a oldalon található kormányzási hiba.
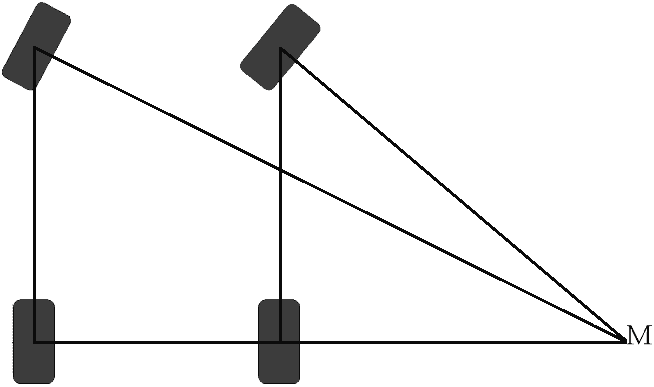
Ez az oldal elmagyarázza, hogyan számítható ki számos adat felhasználásával mindkét első kerék bemeneti szöge (fokban).
A benyújtott szögek kiszámítása:
A megadott szögek kiszámításához a következő járműadatokra van szükség:
- Nyomtáv
- Tengelytávolság
- Fordulókör átmérője
- Kormánycsukló távolság (ezen az oldalon a kormánycsukló távolságát a nyomtávval egyenlőnek tartjuk)
- Gumiabroncsméret (számítástól függően. Ezen az oldalon az abroncsméretet használjuk a számításokhoz, de a lökhárító sarkaiig is lehet számításokat végezni. Azonban további kanyarok kerülnek hozzáadásra).
| Nyomszélesség = 1600 mm | Tengelytáv = 3200 mm |
| A fordulókör átmérője = 13,225 m | Csülök távolság = Nyomtáv = 1600 mm |
| Gumiabroncsméret = 225 | L és L' = ismeretlen |
A szimbólumok magyarázata:
α = Alfa
β = Béta
γ = Gamma
Ezek a betűk a görög ábécéből származnak, és gyakran használják szögszámításokhoz.
L = a hossz
L' = L „ékezet” kiegészítéssel, amelyet gyakran használnak matematikailag. Akár L2-t is írhatott volna. Például egy 3. L-ben két ékezet volt: L”.
Ugyanez vonatkozik R-re is.
Az Alfa, Béta és Gamma szögek az M pontban vannak.
Szög Alfa + Gamma = Béta szög.
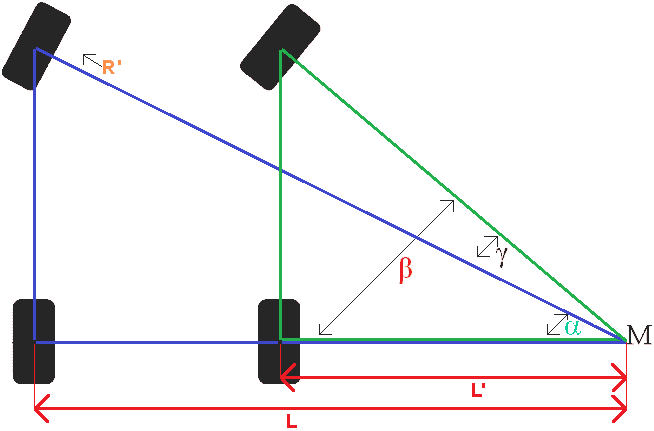
A teljes fordulókör 13,225 6612,5 méter. R a sugár, tehát a félfordulókör (XNUMX). Az ábrán R' látható. Ez az R' nem fix adott. Ezt a sávszélesség felének kivonásával kell kiszámítani. Egy másik módszer a kormánycsukló távolság kivonása, de ezen az oldalon a következőt használjuk: Nyomszélesség = kormánycsukló távolság. Az egyszerű számítás a következő:
R = 6612,5 mm
R' = R – fél sávszélesség
R' = 6612,5 – (225 : 2)
R' = 6612,5 – 112,5
R' = 6500 mm
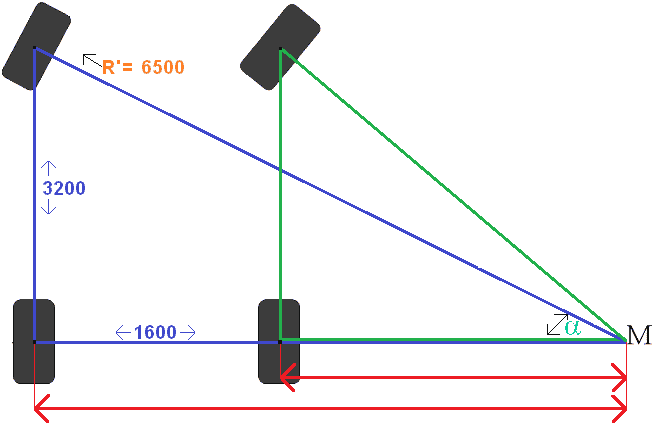
A képen kitöltjük az R' betűt. Ezután a szinuszszabállyal kiszámítjuk a sin α (szinusz Alfa) szöget. Ezután kiszámítjuk a fennmaradó szögeket az Tangens és a Pitagorasz-tétel segítségével.
Szögszámítás a szinusz segítségével:
Sin α = Szemközti oldal: Ferde oldal
Sin α = Wb : R'
Sin α = 3200 : 6500
Sin α = 0.492
Inv Sin α = 29,5°
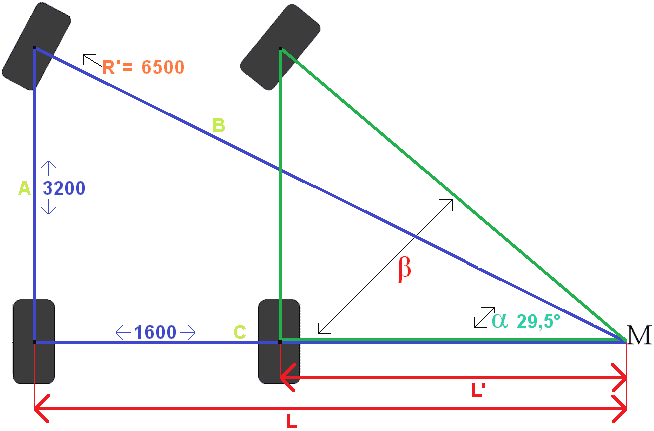
A számítás magyarázata:
Ki akarjuk számítani a Sin α-t. A szinusz az ellenkező oldalt a ferde oldallal osztja fel (mnemonikus: SIN = SOS).
Wb = tengelytáv = 3200 mm. Korábban R' = 6500 mm-t számoltunk.
Ezután ezt felosztjuk; akkor van Sin α = 0.492. A szám szöggé alakításához írja be a sin-1 gombot a számológépbe (általában először nyomja meg a Shift, majd a Sin billentyűt), majd a 0.492-t vagy az ANS gombot. Most a 29,5 fokos szög látható.
A Sin α ma már ismert. Most tulajdonképpen ki akarjuk számítani a tan β-t, de akkor szükségünk van az L' hosszra. Ezt kell először kiszámolni. Ezért az L' számításból származó választ használjuk a Tan β későbbi kiszámításához.
L' = L – Nyomtáv.
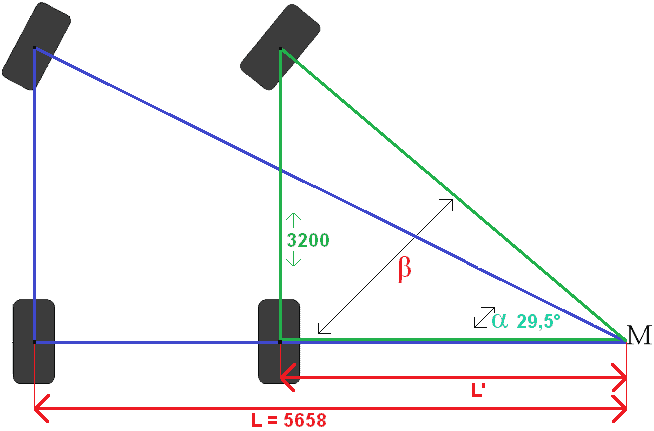
Kiszámítjuk L-t a Pitagorasz-tétel segítségével. A háromszög 2 oldala ismert (6500 és 3200). Az 1600 másik oldala az abroncstól abroncsig futó nyomtáv, tehát nem számít. Kiszámoljuk az alsó oldalt, amely a bal hátsó abroncstól az M közös pontig fut. A számítás tehát a teljes kék háromszögre vonatkozik.
A Pitagorasz-tétel így néz ki:
A^2 + B^2 = C^2. (A ^ jel a „hatalom” szimbóluma. Tehát azt mondja, hogy A négyzet + B négyzet = C négyzet. Itt kissé másképp fogalmazzuk meg.
A 3200 A hosszúságot, a 6500-at B-nek, a legalacsonyabb ismeretlen oldalt pedig C-nek nevezzük:
C^2 = 6500^2 – 3200^2
C^2 = 42250000 – 10240000
C^2 = 32010000^2
A négyzet kiküszöböléséhez vesszük a szám négyzetgyökét.
C^2 = √32010000
C = 5658 mm.
A C oldal valójában L hosszúságú.
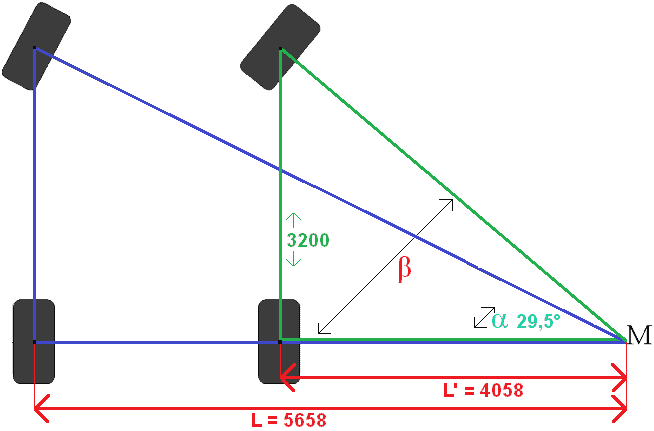
Most már ki lehet számítani L'-t. Az L teljes hossz és a nyomtáv ismert, így a kettő könnyen kivonható egymástól:
L' = L – Nyomtáv
L' = 5658-1600
L' = 4058 mm
Most a Wb és L' ismert. A háromszög három oldala közül kettő ismert, így az érintővel megkeresheti a harmadik oldalt Worden számított:
Szögszámítás az érintővel:
Tan β = Ellenkező oldal : Szomszédos oldal
Tan β = Wb : L'
Tan β = 3200 : 4058
Tan β = 0.789
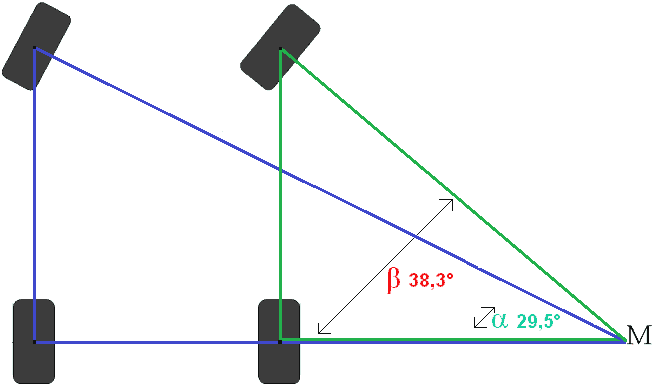
Inv Tan β = 38,3°
A számítás magyarázata:
Tan β-t szeretnénk kiszámítani. Az érintő az ellenkező oldalt a szomszédos oldallal osztja el (mnemonikus: TAN = TOA).
Wb = tengelytáv = 3200 mm. Korábban L' = 4058 mm-t számoltunk.
Ezután ezt felosztjuk; akkor Tan β = 0.789. Ha ezt a számot szöggé szeretné konvertálni, írja be a tan-1 gombot a számológépbe (általában először nyomja meg a Shift, majd a Tan billentyűt), majd a 0.789-et vagy az ANS gombot. Most a 38,3 fokos szög látható.
Most mindkét első kerék kormányszögét kiszámították. A bal első kerék 29,5°-os, a jobb első kerék pedig 38,3°-os szöget zár be. Ez azt jelenti, hogy a kormányszög 8,8°-os eltérést mutat mindkét keréken. Egy balra kanyarban ugyanaz a kormányszög ugyanazzal a kormányzási szöggel történik.
Az oldalon kerék geometriája több kerékállást ismertetnek.
