Aiheet:
- Taivutettu mutkassa
- Lähetettyjen kulmien laskeminen
Taivutus mutkassa:
Etupyörät eivät ohjaudu samassa kulmassa kaarteissa. Sisäpyörä tekee aina "terävämmän" käännöksen kuin ulkopyörä. Kuvassa näkyy, miksi näin on.
Kuvassa näkyy, että etupyörien viivat päättyvät kulmaan M. Kulma M on molempien etupyörien yhteinen kääntöpiste. Jos pyörät kääntyisivät samassa kulmassa (molemmat ovat täsmälleen samassa asennossa), myös pyörien linjat kulkeisivat yhdensuuntaisesti toistensa kanssa äärettömään. He eivät koskaan löydä yhteistä kääntöpistettä M. Siksi ohjausominaisuudet ovat tässä tilanteessa erittäin huonot. Tätä koko periaatetta kutsutaan "toe-out in the bench". Kaikki nykyaikaiset autot on rakennettu tällä ominaisuudella.
Sileillä pinnoilla, esim. pysäköintihallin lattialla, renkaiden vinkumista kuuluu kääntyessä. Tämä johtuu tästä periaatteesta. Sisäpyörä, joka on terävämmässä kulmassa kuin ulompi, kokee jonkin verran luistoa. Tätä kutsutaan ohjausvirheeksi. Lisätietoja ohjausvirheestä (ja kaavio) löytyy sivulta ohjausvirhe.
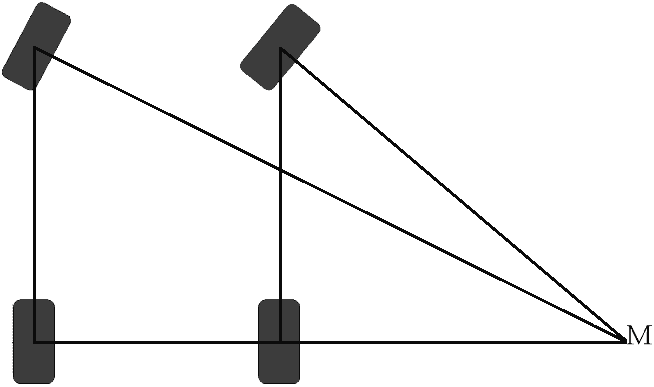
Tällä sivulla selitetään, kuinka molempien etupyörien syöttökulmat (asteina) voidaan laskea useiden tietojen avulla.
Lähetettyjen kulmien laskeminen:
Syötettyjen kulmien laskemiseksi tarvitaan seuraavat ajoneuvotiedot:
- Radan leveys
- Akseliväli
- Kääntöympyrän halkaisija
- Ohjausnivelen etäisyys (tällä sivulla pidämme ohjausnivelen etäisyyden yhtä suurena kuin raideleveys)
- Rengaskoko (riippuen laskennasta. Tällä sivulla laskelmissa käytetään rengaskokoa, mutta laskelmia voidaan tehdä myös puskurin kulmiin asti. Kulmia kuitenkin lisätään).
| Radan leveys = 1600 mm | Akseliväli = 3200 mm |
| Kääntöympyrän halkaisija = 13,225 m | Rystysten välinen etäisyys = raideleveys = 1600 mm |
| Renkaiden koko = 225 | L ja L' = tuntematon |
Symbolien selitykset:
α = Alfa
β = Beta
γ = Gamma
Nämä kirjaimet ovat peräisin kreikkalaisista aakkosista, ja niitä käytetään usein kulman laskemiseen.
L = pituus
L' = L ja "aksentti" lisäyksenä, jota käytetään usein matemaattisesti. Se olisi voinut yhtä hyvin sanoa L2. Esimerkiksi 3. L:ssä oli kaksi aksenttia: L”.
Sama koskee R:tä.
Kulmat Alfa, Beta ja Gamma ovat pisteessä M.
Kulma Alfa + Gamma = Kulma Beta.
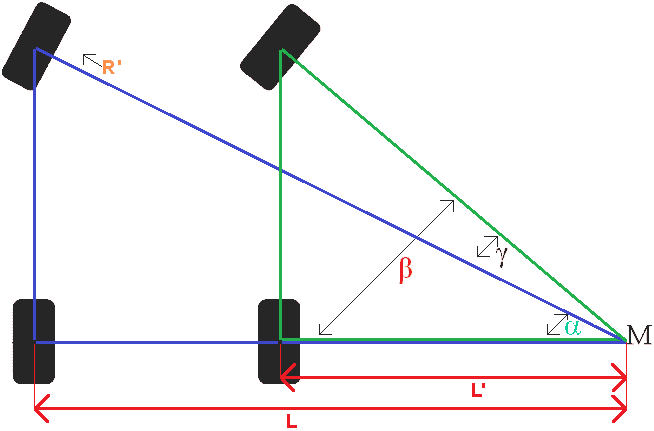
Koko kääntöympyrä on 13,225 6612,5 metriä. R on säde, eli puolikas kääntöympyrä (XNUMX). Kuvassa R' on annettu. Tämä R' ei ole kiinteä tosiasia. Tämä on laskettava vähentämällä puolet kaistanleveydestä. Toinen tapa on vähentää ohjausnivelen etäisyys, mutta tällä sivulla käytämme: Raideleveys = ohjausniveletäisyys. Yksinkertainen laskelma on seuraava:
R = 6612,5 mm
R' = R – puoli kaistanleveyttä
R' = 6612,5 – (225 : 2)
R' = 6612,5 - 112,5
R' = 6500 mm
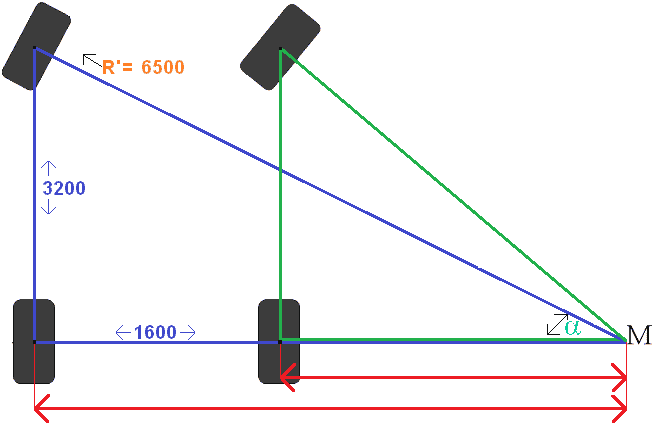
Täytämme kuvan R':n. Laskemme sitten kulman sin α (sini-alfa) sinisäännön avulla. Sitten lasketaan loput kulmat Tangentin ja Pythagoraan lauseen avulla.
Kulman laskenta sinillä:
Sin α = Vastakkainen puoli: Vino puoli
Sin α = Wb : R'
Sin α = 3200 : 6500
Sin α = 0.492
Inv Sin α = 29,5°
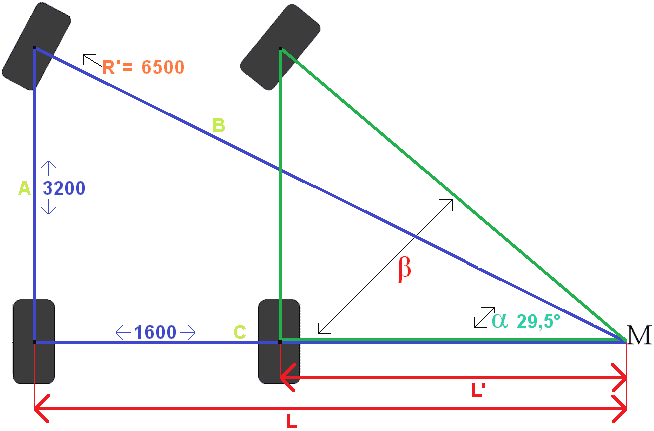
Laskennan selitys:
Haluamme laskea Sin α. Sinus on jaettu vastakkaiselle puolelle vinolla puolella (muistomerkki: SIN = SOS).
Wb = akseliväli = 3200 mm. Aiemmin laskettiin R' = 6500 mm.
Jaamme sen sitten yhteen; niin meillä on Sin α = 0.492. Muuntaaksesi tämän luvun kulmaksi, syötä sin-1-painike laskimeen (paina yleensä ensin Shift-painiketta ja sitten Sin-näppäintä) ja sen jälkeen 0.492 tai ANS-painike. Nyt näkyy 29,5 asteen kulma.
Sin α tunnetaan nyt. Nyt haluamme itse asiassa laskea tan β, mutta silloin tarvitsemme pituuden L'. Tämä on ensin laskettava. Siksi käytämme laskelman L' vastausta myöhemmin Tan β:n laskemiseen.
L' = L – raideleveys.
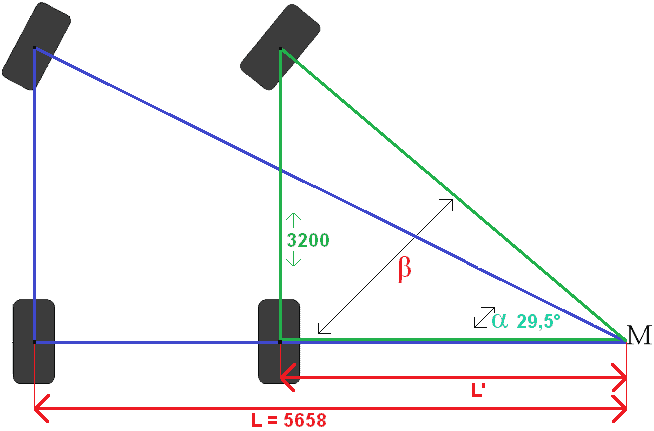
Laskemme L käyttämällä Pythagoraan lausetta. Kolmion 2 sivua tunnetaan (6500 ja 3200). 1600:n toinen puoli on raideleveys, joka kulkee renkaasta renkaaseen, joten sitä ei lasketa. Aiomme laskea alapuolen, joka kulkee vasemmasta takarenkaasta yhteiseen pisteeseen M. Laskelma koskee siis koko sinistä kolmiota.
Pythagoraan lause näyttää tältä:
A^2 + B^2 = C^2. (Etumerkki ^ on "vallan" symboli. Se sanoo siis A neliö + B neliö = C neliö. Muotoilemme sen tässä hieman eri tavalla.
Kutsumme pituutta 3200 A, 6500 B:ksi ja alinta tuntematonta puolta kutsumme C:ksi:
C^2 = 6500^2 – 3200^2
C^2 = 42250000 – 10240000
C^2 = 32010000^2
Neliön poistamiseksi otamme luvun neliöjuuren.
C^2 = √32010000
C = 5658 mm.
Sivu C on itse asiassa pituus L.
Nyt L' voidaan laskea. Täyspituus L ja raideleveys ovat tiedossa, joten nämä kaksi voidaan helposti vähentää toisistaan:
L' = L – raideleveys
L' = 5658 - 1600
L' = 4058 mm
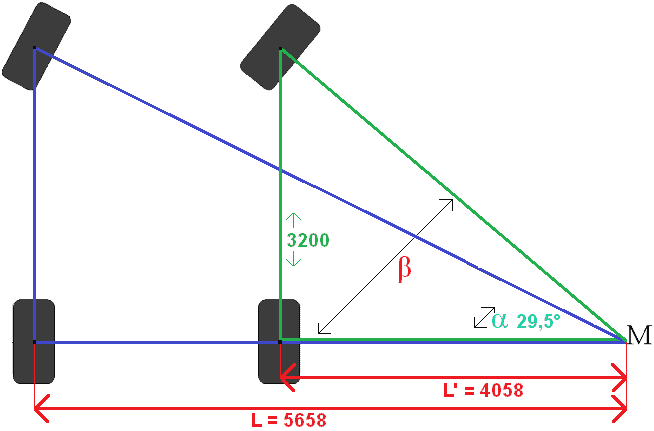
Nyt Wb ja L' tunnetaan. Kolmion kolmesta sivusta kaksi tunnetaan, joten voit käyttää Tangenttia löytääksesi kolmannen sivun Worden laskettu:
Kulman laskenta tangentilla:
Tan β = Vastakkainen puoli : Viereinen puoli
Tan β = Wb : L'
Tan β = 3200:4058
Tan β = 0.789
Inv Tan β = 38,3°
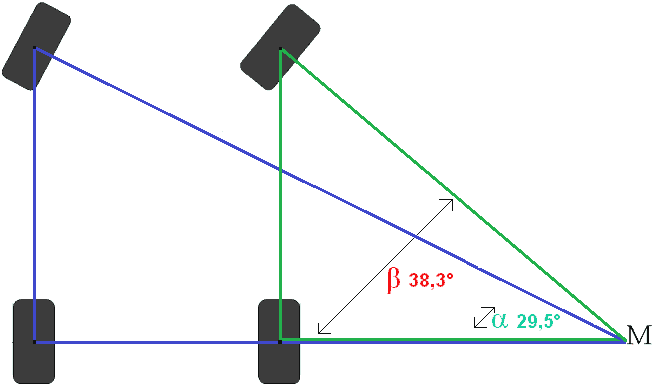
Laskennan selitys:
Haluamme laskea Tan β. Tangentti jakaa vastakkaisen puolen viereisellä puolella (muistomerkki: TAN = TOA).
Wb = akseliväli = 3200 mm. Aiemmin laskettiin L' = 4058 mm.
Jaamme sen sitten yhteen; niin meillä on Tan β = 0.789. Muuntaaksesi tämän luvun kulmaksi, syötä tan-1-painike laskimeen (paina yleensä ensin Shift-painiketta ja sitten Tan-näppäintä) ja sen jälkeen 0.789 tai ANS-painiketta. Nyt näkyy 38,3 asteen kulma.
Nyt on laskettu molempien etupyörien ohjauskulmat. Vasen etupyörä on 29,5° kulmassa ja oikea etupyörä 38,3° kulmassa. Tämä tarkoittaa, että ohjauskulman ero molemmissa pyörissä on 8,8°. Vasemmalle käännettäessä saadaan sama ohjauskulma samalla ohjauskulmalla.
Sivulla pyörän geometria useita pyörän asentoja kuvataan.
