Rolling circumference calculator:
Installing the wrong tire size under a car will result in a discrepancy on the speedometer. The exact deviation can be calculated with the calculator below. When using a mobile phone, it is best to rotate the device to “landscape mode” to bring the entire table into view.
The table displays two tire sizes: 205/55R16 and 225/40R18. These values can be changed to other sizes you wish to compare. At the bottom, the speeds of both tire sizes are compared: if tire 1 is rotating at speed x, then tire 2 rotates at speed y. This calculator is designed for European standaards: millimeters and kilometers per hour. For the translated version, the km/h automatically converts to mph.
Because tire sizes are initially compared statically, the suspension can remain at the preselected 0% and 0 mm. The result will display as N/A.
The explanation of static and dynamic height and circumference (with a load >0) will be given in the following paragraphs. For the static comparison, the RFT (RunFlat Tyre) has no impact on the calculation. The deflection of a RunFlat tire only becomes relevant when looking at dynamic properties.
Explanation about tire height and rolling circumference:
Using the calculator, the tire height and rolling circumference can be calculated. This is ideal when searching for a different tire size (for example, increasing from 16 to 18 inches) that fits the car without affecting the accuracy of the speedometer.
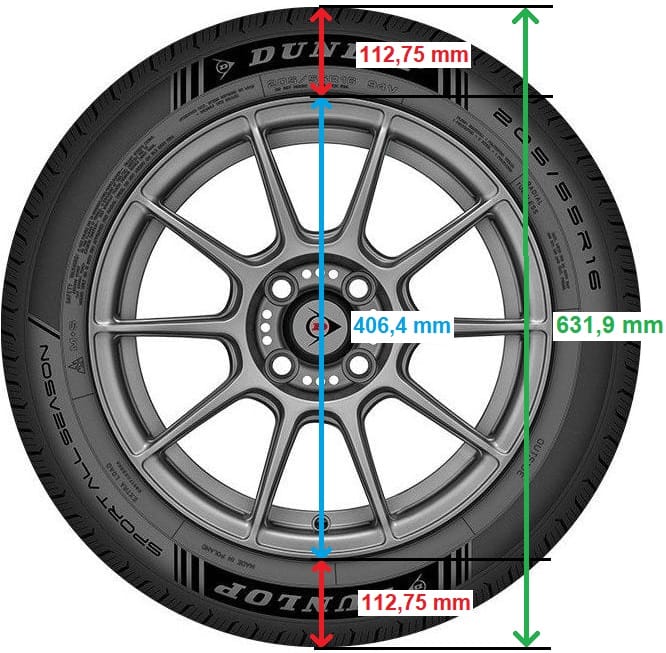
The tire in the example is marked: 205/55 R16:
- 205 = tread width in mm
- 55 = tire sidewall height from the road to the underside of the rim = 55% of 205 (0.55 x 205 = 112.75 mm)
- 16 = rim diameter in inches (1 inch = 25.4 mm, so 16 inches x 25.4 mm = 406.4 mm)
Enter these three values into the calculator to determine the tire height and static rolling circumference in an unloaded condition. Tire height equals twice the sidewall height in millimeters, plus the rim diameter in mm. In the example above: 112.75 + 112.75 + 406.4 = 631.9 mm (or 63.19 cm). With this calculator, it’s easy to calculate the tire heights of different tire sizes and the difference in circumference and speed.
The two tire sizes shown by default in the table, the 205/55 R16 and the 225/40 R18, have very little difference in height and circumference. This means the speed difference on the speedometer is also minimal. Therefore, if the manufacturer specifies 205/55 R16 as the standard size, mounting wheels with tires size 225/40 R18 is also allowed. The only question is whether the wider tires will rub against the wheel arches. If this occurs during steering, it can cause excessive tire wear and is a reason for rejection during the vehicle inspection (APK). In that case, wheel spacers offer a solution.
More information about tires can be found on the wheels and tires page.
Static rolling circumference:
The static rolling circumference is the distance a wheel travels after one complete rotation when rolled over the ground without a load, so without the vehicle’s weight resting on it. There is no deformation from suspension or any type of load.
For example, if a 205/55 R16 tire size is installed (from the factory) and someone wants to install larger rims and tires, there are several points to consider. The offset (ET value) must be correct, the tires must not rub against the shock absorber, wheel well, or control arms, and the static rolling circumference should not differ too much compared to the other tire size. The static rolling circumference can be calculated using this calculator. As described above, we assume a suspension of 0% and 0 mm when calculating static rolling circumference. The calculations for determining the static rolling circumference of a wheel are provided below.
- Tire size: 205/55 R16
- Calculation of sidewall height: 205 × (55/100) = 112.75 mm
- Calculation of total tire diameter: The total tire diameter is the sum of the rim diameter and twice the sidewall height:
– Total diameter = (rim diameter in inches × 25.4) + 2 × sidewall height
– The rim diameter in millimeters is: 16 × 25.4 = 406.4 mm
– So the total diameter is: 406.4 + 2 × 112.75 = 631.9 mm - Calculation of static rolling circumference: The circumference of the tire is calculated using the formula for the circumference of a circle:
Rolling circumference = π × total diameter
Rolling circumference = π × 631.9
Rolling circumference = 1984.76 mm ≈ 1.98 meter
The tire size 205/55 R16 has a static rolling circumference of approximately 1.98 m. If you mark the sidewall of the tire and the road with chalk, drive the wheel for one full revolution, and then mark the road at the height of the mark on the sidewall, the distance between these marks will be 1.98 meters. This distance determines the speed shown on the vehicle’s speedometer.
If we now compare the 225/40 R18 tire size, the rolling circumference is 2.00 m. This difference is minimal, making this tire size suitable for the car (as long as it doesn’t rub anywhere). However, if the 225/45 R18 size is calculated, the static rolling circumference is 2.07 m. Compared to the 205/55 R16, this is too much of a difference, so a lower speed would be indicated on the speedometer (it takes the wheel longer to complete one revolution). Therefore, this tire size is not recommended for installation.
The owner’s manual or websites such as Autoweek.nl can be used to find out which tire sizes are approved for the car. With this calculator, various tire sizes can be compared.
Dynamic rolling circumference:
The dynamic rolling circumference of a tire is the distance the tire covers in one complete rotation under normal operating conditions. Here, the tire is under the vehicle’s load and in contact with the road. Tire deformation causes a difference between the static and dynamic rolling circumference. The dynamic rolling circumference is, in practice, almost always smaller than the static rolling circumference.
In practice, this difference can have noticeable effects. When two tires on the same axle have different pressures, differences in tire height and rolling circumference occur. This can lead to pulling to one side or a misaligned steering wheel. If all tires have the same, but too low air pressure, the vehicle won’t pull to one side, but the speed display may vary due to the changed rolling circumference.
In the calculator, the dynamic rolling circumference is only calculated when the suspension value is greater than 0. The suspension can be entered either as a percentage or as an absolute value in millimeters. For a realistic result, it’s important to enter only one of these values. If both a percentage and a value in millimeters are entered, they are added together, making the outcome less realistic.
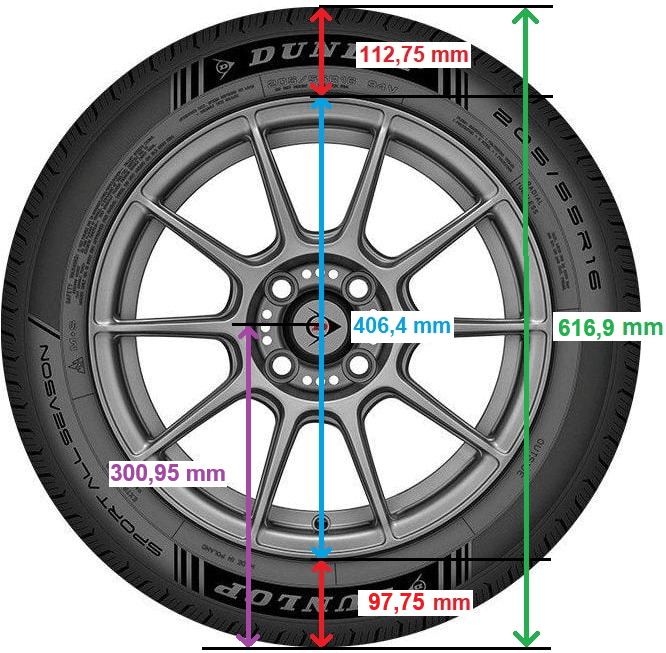
In this example, we use a tire size of 205/55R16. The static wheel diameter is 631.9 mm. Under load, the tire deflects 15 mm at the bottom. This decreases the total wheel diameter:
- Static condition: 631.9 mm
- Deflection: 15.0 mm
- Dynamic condition: 616.9 mm
The dynamic rolling circumference is then calculated as follows:
- Rolling circumference = π × dynamic diameter
- Rolling circumference = π × 616.9 ≈ 1938 mm (≈ 1.94 m)
For comparison: the static rolling circumference is about 1.98 m. This difference explains why load and tire pressure influence the speed readout on the speedometer. In this example, a speed of 100 km/h results in a deviation of about 2.37 km/h due to the 15 mm deflection.
Suspension as a percentage and the k-factor:
When suspension is entered as a percentage, the calculation becomes more theoretical. It cannot be assumed that, for example, a 10% suspension deflection means the entire sidewall height decreases by 10%. The sidewall height is measured from the bead to the tread, but the sidewall section next to the rim hardly deflects at all.
The sidewall is also stiffer near the shoulder transition. In a simplified approach, it can be assumed that about 25 mm of the sidewall height barely or does not compress. With a 205/55R16 tire with a static sidewall height of 112.75 mm and a static wheel diameter of 631.9 mm, the dynamic height at 10% suspension can be calculated as follows:
- Dynamic height = static wheel height − ((static sidewall height − 25) × (percentage suspension / 100)) − suspension in mm
- Dynamic height = 631.9 − ((112.75 − 25) * (10 / 100)) − 0
- Dynamic height = 623 mm
With this dynamic height of 623 mm, the rolling circumference can then be recalculated. If, instead of a percentage, an absolute suspension value in millimeters is entered, only the last part of the formula changes. With a suspension of 30 mm and 0% percentage suspension, this results in:
- Dynamic height = 631.9 − ((112.75 − 25) * (0 / 100)) − 30
- Dynamic height = 601.9 mm
To make this percentage-based calculation more realistic, the calculator uses a k-factor. The k-factor determines which part of the sidewall height is actually deformable. With low-profile tires the sidewall is stiffer and the k-factor is lower. With taller-profile tires, the sidewall is more flexible and the k-factor is higher. For example, if a k-factor of 0.70 is used for this tire (suitable for a mid-profile tire), the deformable sidewall height is calculated as follows:
- Deformable sidewall height = sidewall height * k
- Deformable sidewall height = 112.75 * 0.70
- Deformable sidewall height = 78.9 mm
Only this part of the sidewall height is used when calculating percentage-based suspension deflection. At 10% suspension deflection, this results in:
- Compression from percentage suspension = 78.9 * (10 / 100)
- Compression from percentage suspension = 7.9 mm
Dynamic wheel diameter is then:
- Dynamic height = 631.9 − 7.9 = 624.0 mm
The total compression due to suspension consists of two parts: a percentage deflection applied over the deformable sidewall height, and an absolute deflection in millimeters:
- Compression = (deformable sidewall height * (percentage suspension / 100)) + suspension in mm
When entering a suspension value as an absolute number in millimeters, directly observed or estimated deformation is entered. In this case, the k-factor is not used. For the most realistic result, it is important to enter only one of these values (percentage or millimeters). When both are used, they are added together and the outcome may deviate from practice.
Runflat (RFT)
Additionally, RFT can be selected in the calculator. A runflat tire has a stiffer sidewall construction and deflects less under the same load than a standard tire. Therefore, the calculated suspension for an RFT tire is multiplied by a factor of 0.8:
- RFT suspension = suspension * 0.8
As a result, the dynamic diameter and rolling circumference are slightly larger than on a non-runflat tire under the same conditions.
Conclusion:
When comparing various tire sizes with the rolling circumference calculator, the practice is to look at the static data. Although a wider tire or rim influences the weight distribution over the road and thus the amount of tire deflection, these differences are so small in most situations that they can be neglected when comparing tire sizes.
However, entering dynamic data, such as a percentage or an absolute suspension value in millimeters, provides a more realistic picture of the real situation under load. When entering a percentage suspension value, the k-factor is also taken into account, further improving the realism of the results. These data show how tire deformation affects the dynamic rolling circumference and thus the speed shown on the speedometer.
Related page:
