Introduction:
This page explains how to balance reaction equations. A reaction equation is a formula where the substances before and after combustion are filled in (for example, C and O2). After combustion, these substances will have formed into CO2.
Next, with the aid of this reaction equation, the amount of air required to burn 1 kilogram of the given substance is determined.
Reaction Equation C and O2:
Below is the reaction equation of C and O2. Further on, it will be explained how to fill in this equation.
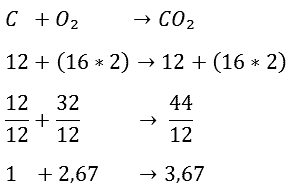
We start with the top line. In the equation, the carbon atom (C) together with the oxygen atoms (O2) is on the left side of the arrow. These substances must be burned. The arrow indicates how the compounds of substances are after combustion. In the equation, it is now seen that one carbon atom and two oxygen atoms together form carbon dioxide (CO2).
The next step is to determine the atomic masses of C and O2. Each isotope of a chemical element has a different atomic mass, expressed in grams per mole. The atomic masses of carbon and oxygen are given:
C = 12g/mol
O = 16g/mol
First, the reaction equation of the combustion of C and O2 is given:
Next, the atomic masses are noted. Under C, 12 is placed, and under O2 (16×2), because O2 consists of two oxygen atoms each weighing 16 grams per mole.
On the right side of the arrow, the C atom is added to the oxygen atoms. This totals to 44. The next step is to calculate how many kilograms of oxygen are needed to burn one kilogram of carbon. This is done by dividing the entire equation by 12.
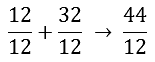
After dividing by 12, the following numbers remain:
Now it actually reads:
We want it in kilograms and not in grams per mole. In principle, you can simply replace g/mol with kg because you can consider it as ratios.
An example:
You need to add 1 liter of cleaning agent to 10 liters of water. (One-tenth of a cleaning agent per liter of water.) This means that per 10 hectoliters of water, 1 hectoliter of the agent must also be added. Or 10 centiliters of water and 1 centiliter of cleaning agent, but then you will have to mix this 100 times to reach 10 liters of water per 1 liter of cleaning agent again. The ratios remain the same.
The conclusion is that grams per mole and kg can be exchanged as long as there are no other magnitudes in the formula!
In the equation, it is now seen that 2.67 kg of O2 is needed to burn 1 kg of C. This produces 3.67 kg of CO2. You can easily check for any calculation errors by comparing the numbers to the left and right of the arrow. By adding up the numbers to the left of the arrow, you reach 3.67, just like the number to the right of the arrow, so this is executed correctly. Especially in long reaction equations, it is useful to check yourself in this way.
Reaction Equation H2 and O2:
The reaction equation of H2 and O2 is established as above with CO and O2. Balancing the reaction equation now works slightly differently.
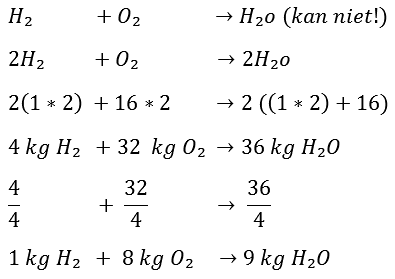
We start again at the beginning; H2 and O2 will form H2O after combustion, but the first problem arises here:
When you were to add H2 and O2 together, you would get H2O2. This is not water but hydrogen peroxide. Obviously, that is not the intention. This is the point where the reaction equation must be balanced because H2O should ultimately be formed. What needs to be done now is to double the number of hydrogen atoms. We do this as follows. By now placing a 2 in front of the H2, you have (2xH2) = 4 hydrogen atoms.
On the right side of the arrow, the same applies, but now the O is also multiplied by 2. Because the following holds true:
2H2O = 2(H2O) = 2xH2 and 2xO2.
Now you have the two oxygen atoms back, only including 4 hydrogen atoms. This shows that you cannot just add up the atoms because a chemical compound of hydrogen peroxide will form instead of water.
The next step is calculating the atomic masses. For the next step, it is important to calculate the atomic masses of H and O2. The atomic masses of carbon and oxygen are given:
H = 1g/mol
O = 16g/mol
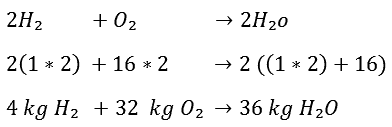
It is now required to have 32 kg of O2 to burn 4 kg of H2. After combustion, 36 kg of H2O are produced. By now dividing the entire equation by 4, it can be determined how many kg of O2 are needed to burn 1 kg of H2:
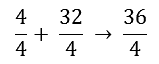
Eventually, it becomes:
So to burn 1 kg of hydrogen, 8 kg of oxygen is needed.
