Subjects:
- General
- Reaction equation C and O2
- Reaction equation H2 and O2
General:
This page explains how to make a reaction equation correct. A reaction equation is a formula in which the substances before and after combustion are entered (eg C and O2). After combustion, these substances will have formed into CO2.
Then, using this reaction equation, it is determined how many kilograms of air are needed to burn 1 kilogram of the substance in question.

Reaction equation C and O2:
Below is the reaction equation of C and O2. Further on, it is explained how filling in this equation is accomplished.
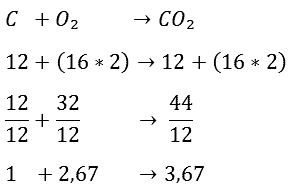
We'll start with the top line. In the equation, the carbon atom (C) along with the oxygen atoms (O2) is on the left side of the arrow. These substances must be incinerated. The arrow indicates the connection between the substances after combustion. The equation now shows that one carbon atom and two oxygen atoms together form carbon dioxide (CO2).
For the next step, it is important to determine the atomic masses of C and O2. Each isotope of a chemical element has a different atomic mass, which is expressed in grams per mole. The atomic masses of carbon and oxygen are given:
C = 12 g/mol
O = 16 g/mol
First the reaction equation of the combustion of C and O2 is given:
Then the atomic masses are noted. 12 is placed below C and below O2 (16×2), because O2 consists of two atoms of oxygen of 16 grams per mole each.
On the right side of the arrow, the C atom is added to the oxygen atoms. This adds up to 44. In the next step, it is calculated how many kilograms of oxygen are needed to burn one kilogram of carbon. We do this by dividing the entire equation by 12.
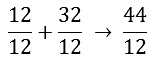
After dividing by 12, the following numbers remain:
Now it actually says:
We want it in kilograms and not grams per mole. In principle, you can simply replace g/mol with kg, because you can see it as proportions.
An example:
You need to add 10 liter of detergent to 1 liters of water. (A tenth of detergent per liter of water.) This means that for every 10 hectoliters of water, 1 hectolitre of that agent must also be added. Or 10 centiliters of water and 1 centilitre of detergent, but then you will have to mix this 100 times in succession to get the 10 liters of water per 1 liter of detergent again. The proportions remain the same.
The conclusion is that grams per mole and kg can be interchanged, as long as there are no other quantities in the formula!
The equation now shows that it takes 2,67 kg of O2 to burn 1 kg of C. This produces 3,67 kg of CO2. You can easily check whether a calculation error has been made by comparing the numbers to the left and right of the arrow. Adding up the numbers to the left of the arrow gives you 3,67, just like the number to the right of the arrow, so this is well done. Especially with long reaction equations it is useful to check yourself in this way.
Reaction equation H2 and O2:
We set up the reaction equation of H2 and O2 as it was done above with CO and O2. Making the reaction equation correct is now a bit different.
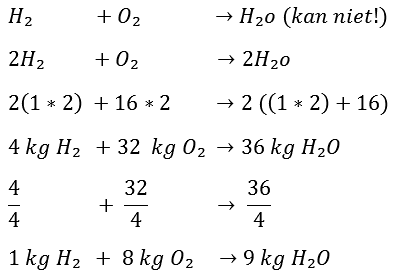
We start again at the beginning; H2 and O2 will be formed into H2O after combustion, only the first problem is there:
If you added H2 and O2 together, you would get H2O2. This is not water, but hydrogen peroxide. That is of course not the intention. This is the point at which the reaction equation must be made right, because eventually H2O must be formed. What needs to be done now is to double the number of hydrogen atoms. We do this as follows. By now putting a 2 in front of the H2, you have (2xH2) = 4 hydrogen atoms.
The same applies to the right side of the arrow, but now the O is also multiplied by 2. Because the following applies:
2H2O = 2(H2O) = 2xH2 and 2xO2.
So now you have the two oxygen atoms back, only including 4 hydrogen atoms. So you can see that you can't just add the atoms together, because then a chemical compound of hydrogen peroxide is created instead of water.
The next step is to calculate the atomic masses. For the next step, it is important to determine the atomic masses of H and O2. The atomic masses of carbon and oxygen are given:
H = 1g/mole
O = 16 g/mol
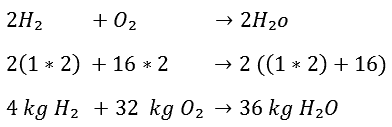
It now takes 32 kg of O2 to burn 4 kg of H2. 36 kg of H2O is formed after combustion. Now, by dividing the entire equation by 4, it can be determined how many kg O2 are needed to burn 1 kg H2:
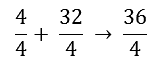
In the end it becomes:
So to burn 1 kg of hydrogen, 8 kg of oxygen is needed.
