Subject:
Pressure in a hydraulic system:
Hydraulic systems operate according to the laws of hydrostatics. Pascal’s Law states: “The pressure in a compressed, stationary fluid is transmitted equally in all directions within a closed system.”
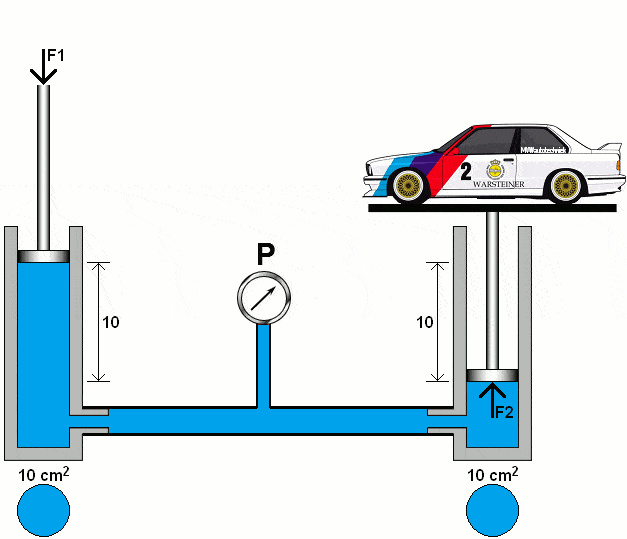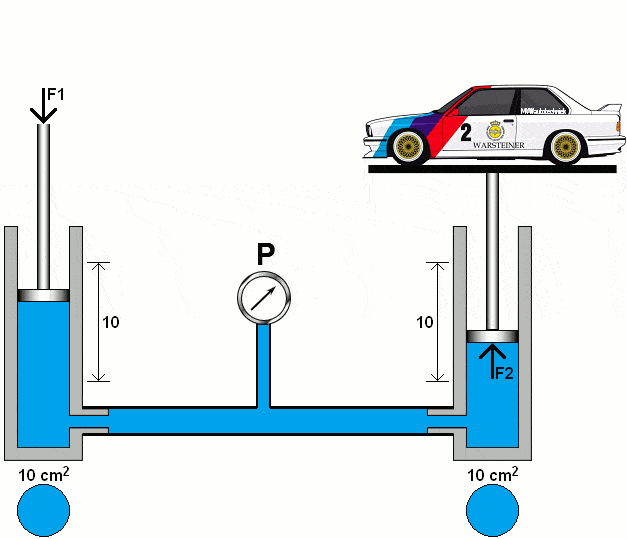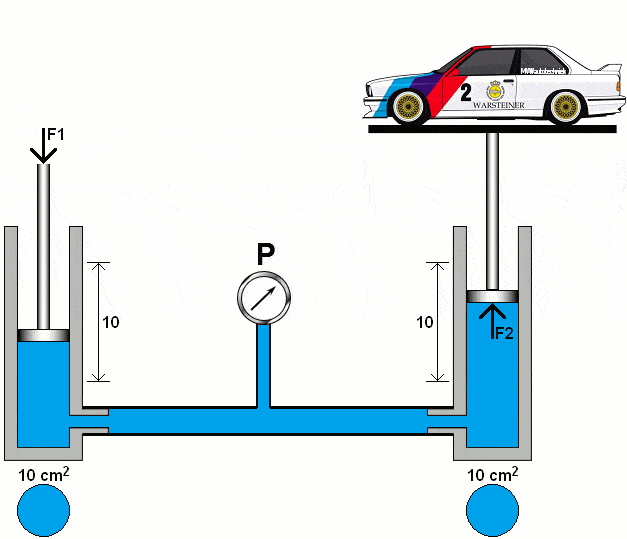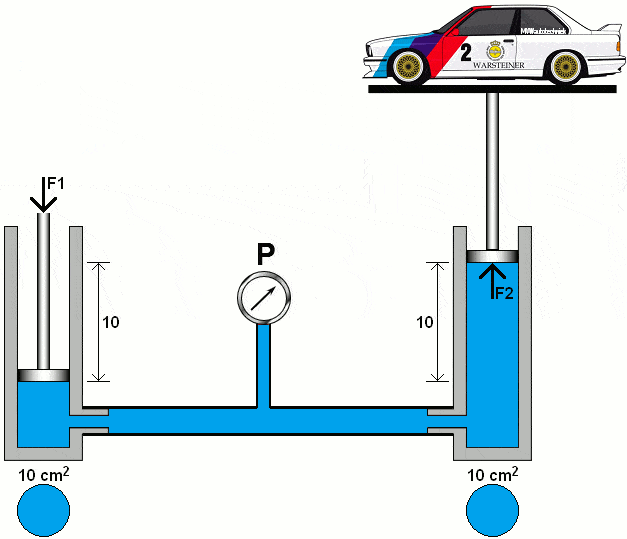
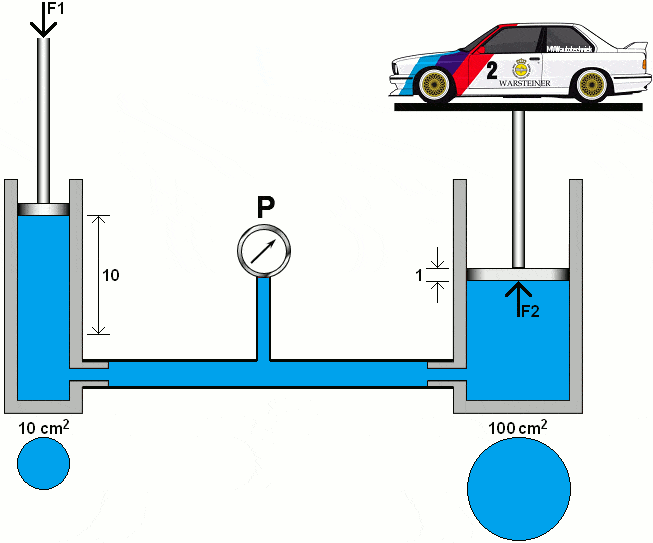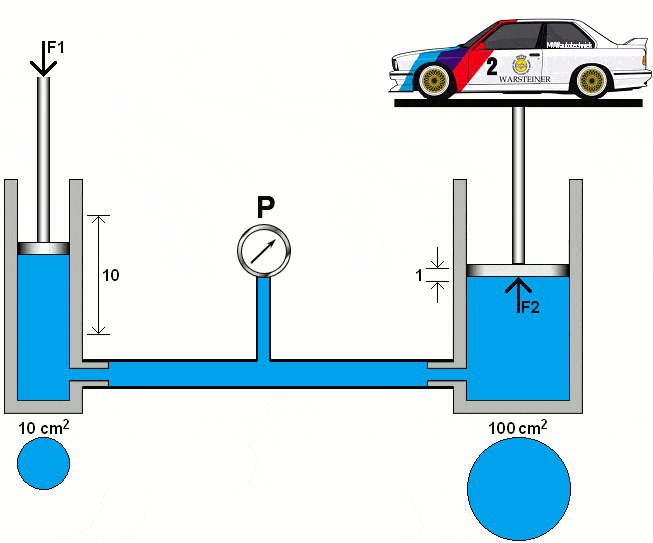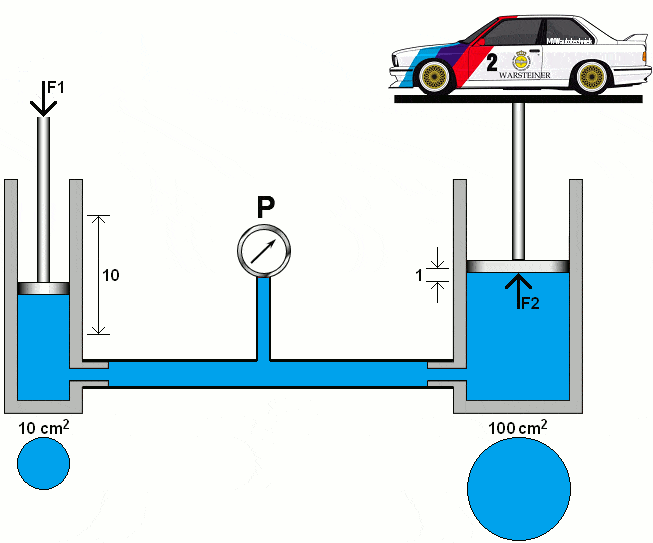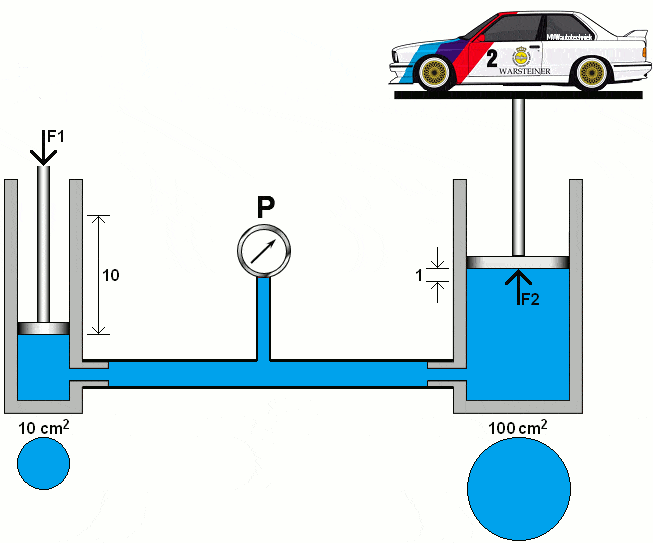
The following animation demonstrates the principle of a hydraulic system with two pistons, lines with a pressure gauge, and oil (colored blue).
The left piston is pushed downward with a certain force (F1). As a result of the fluid displacement in the left piston, the right piston is pushed upward with force (F2). The diameters of both cylinders are the same. In this section, we will calculate the pressures and forces in two hydraulic systems.
To calculate the force F2, we first need to determine the weight (kg) and the gravitational acceleration (m/s²). The weight of the fictional BMW is 1000 kg. We round the gravitational acceleration to 10. With these values, we enter the formula to calculate the required force:
The following formula can be used to calculate the pressure indicated by the pressure gauge:
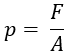
Where:
- p = pressure in Pa (Pascal)
- F = force in N (Newton)
- A = area in m²
We enter the values into the formula to calculate the fluid pressure under both pistons.
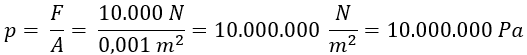
A helpful reminder:
- 1 kPa (kilopascal) = 1,000 Pa;
- 1 MPa (megapascal) = 1,000,000 Pa;
- 1 bar = 100,000 Pa = 100,000 N/cm².
A pressure of 10,000,000 Pa is therefore equal to 100 bar.
In the following animation, the diameter of the right piston is increased tenfold. We calculate the pressure under the right piston using the area (A2) of 100 cm².
The fluid pressure is the same throughout the entire system. We enter the pressure into the following formulas:
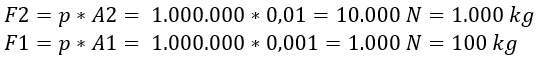
The formulas show that the 1000 kg car can be lifted with a force (F1) on the left piston of 100 kg. The distance traveled by the left piston is, in proportion, ten times greater than that of the right piston.
By entering the following calculation, we can demonstrate that the pressure is the same throughout the entire system:
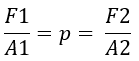
Related page:
