Thevenin

Subjects:

Thevenin replacement schedule
Scheme 1
Scheme 2

Thevenin replacement schedule:
The Thevenin theorem is a widely used tool for simplifying complex circuits. Any circuit with one or more voltage sources with a number resistors, can be replaced by 1 voltage source Eth and 1 internal resistance Rth. The Eth and Rth that are calculated are important to ultimately determine the voltages across the resistors and the current through the circuit.

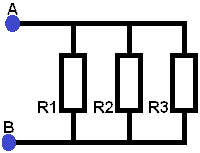
Scheme 1:
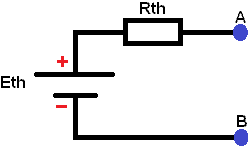
A Thevenin replacement diagram is shown opposite. Eth stands for the voltage source and Rth for the replacement resistor. Any scheme with multiple voltage sources and multiple resistors can be simplified to this scheme.

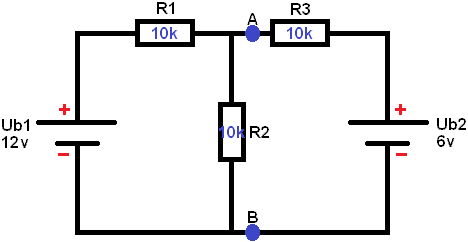
This scheme with 2 voltage sources and 3 resistors is calculated and simplified to the Thevenin replacement scheme. In the following steps, the voltages and currents in the scheme are calculated to determine the voltage UAB (the voltage at points A and B).

Step 1:
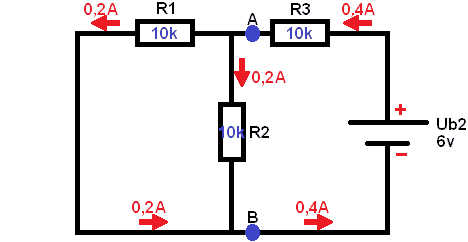
Particular replacement resistance of the diagram below where UB2 is shorted. The formulas show the effect of the replacement resistance and the current.

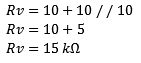
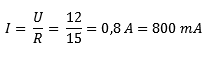
Short-circuit one voltage source. In this case Ub2 (see image below). Remove the voltage source from the schematic. The current of 1 A starts to flow from the voltage source Ub0,8. First, the voltage across resistor R1 must be calculated, as the current encounters it first.

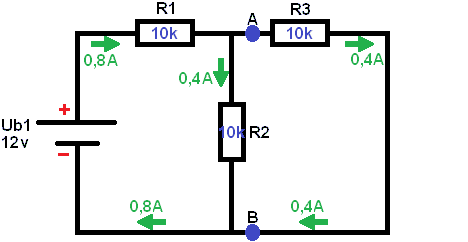
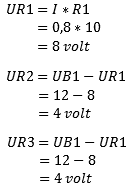
It is important not to calculate UR2 the same as UR1, because the voltage UR1 has yet to be subtracted from it. This is because the voltage is lost by the consumers. In the beginning of the diagram the voltage is 12 Volts, but when the minus is reached, the voltage should be 0 Volts. This is not the case with electricity! All current that leaves the battery is distributed over the entire scheme and comes back together at the negative of the battery.

Step 2:
Here Ub1 has now been removed from the scheme and Ub2 has been replaced. Now the replacement resistance and current due to Ub2 need to be determined.

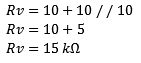
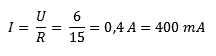
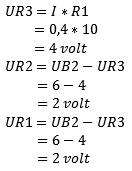
Step 3:
Now it's time to restore the schematic back to its original state:

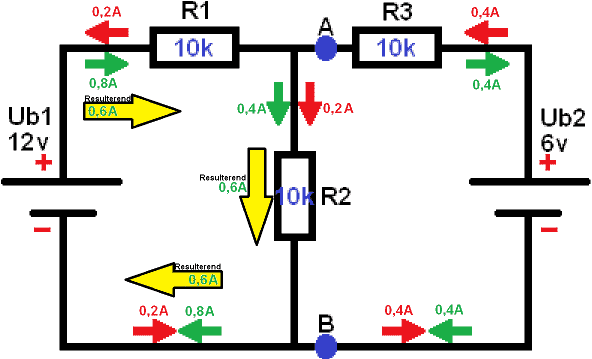
The flow direction of both schemes is displayed; the green from the first and the red from the second scheme. If the flow direction is opposite to each other (the arrows point towards each other), then a resulting flow will remain.
0,2 A to the right and 0,8 A to the left: Causes 0,6 A to go to the left (by simply subtracting 0,8 and 0,2).
0,4 A to the right and 0,4 A to the left: cancel each other out. The resulting current is 0.

The current across resistor R2 is known. Now the voltage UAB can be measured. The voltage UAB is parallel to R2, so they are the same. In principle, the resulting voltage across R2 is now also measured: UAB = UR2.

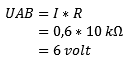
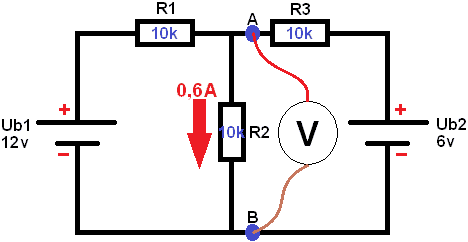
Step 4:
To create a Thevenin replacement scheme, step 4 still needs to be performed. UAB open is known. This is also called the open terminal voltage, Eth or Uth (Eth is used in this calculation example). Eth represents the Thevenin voltage.

Calculate Rth:

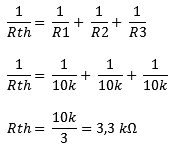
Eth is known. So in the final Thevenin substitution scheme, Eth and Rth should be indicated:
The diagram below shows the Thevenin replacement schedule as it is officially intended. Any scheme with one or more voltage sources and resistors can be simplified to this scheme:

Eth = 6 volts
Rth = 3,3 kΩ

Scheme 2:
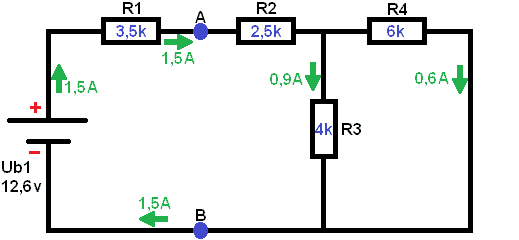
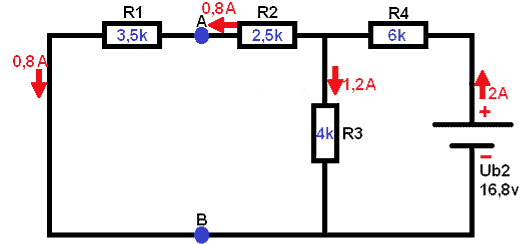
Below is a diagram with 2 voltage sources (Ub1 of 12,6v and Ub2 of 16,8v). The voltage UAB must be determined (i.e. the voltage on the blue dots). The following steps calculate the voltages across the resistors and the currents throughout the scheme. Subsequently, the voltage across A and B can again be calculated.

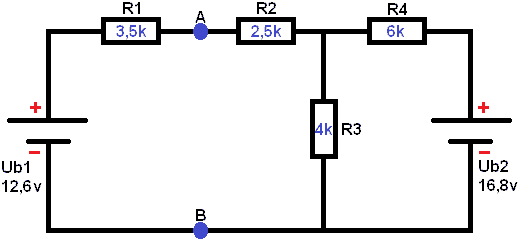
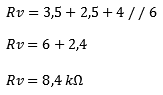
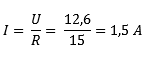
Short circuit 1 voltage source. In this case Ub2. Remove the voltage source from the schematic. The current of 1 A starts to flow from the voltage source Ub1,5. First, the voltage across resistor R1 must be calculated, as the current encounters it first.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit elit, luctus nec ullamcorper mattis, dapibus leo pulvinar.

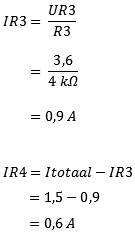
Step 2:
Determine the replacement resistance from the diagram below. Here Ub1 has now been removed from the scheme and Ub2 has been replaced. In this case, the replacement resistance is again

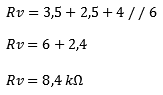
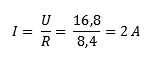
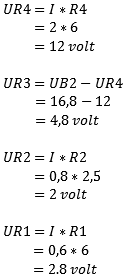
Step 3:
Now it's time to restore the schematic back to its original state:

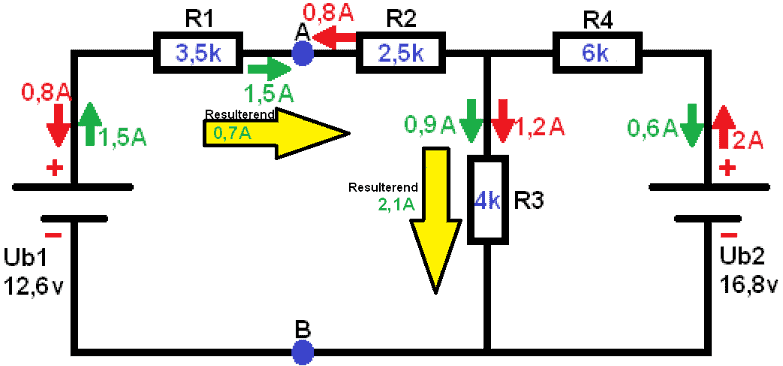
With this data the voltage UAB can be calculated. A current of 0,7mA flows across the resistor R1 of 3,5kΩ. Since the left part of the diagram (the part of Ub1) is a closed circuit, UAB is calculated with the voltage of Ub1. Ub2 does not participate now, because this is another closed circle. This is easy to see by applying Kirchhoff: All voltages in a closed circuit are equal to 0. We can prove that:

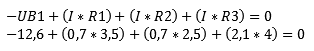
Calculating voltage UAB: