Subjects:
- thermistor
- PTC resistance
- NTC resistance
- Determining the NTC characteristic
thermistor:
A thermistor is a name for a component that has a resistance value that depends on the temperature. The English word is a combination of the words thermal and resistor. Thermistors are used in automotive technology, among other things, as temperature sensors en overload protections.
Thermistors can be divided into 2 groups; namely that the resistance value increases with increasing temperature (PTC) or that the resistance value decreases with increasing temperature (NTC). The terms NTC and PTC are further explained below.
PTC resistance:
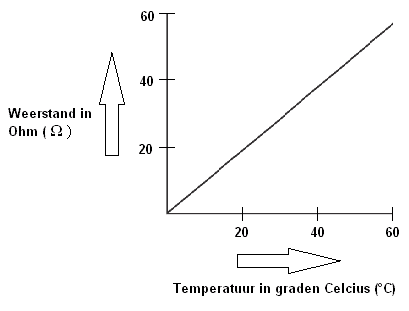
A PTC resistor is a resistor with a Positive Temperature Coefficient. They are mainly used as temperature protection in electrical appliances. As the temperature increases, the resistance also increases. The relationship between resistance and temperature has a linear relationship with a PTC resistance. That is, the resistance increases proportionally with the temperature increase. This can be seen in the image below from the exact straight line.
PTC resistors are used, among other things, for mirror heating. Without this protection resistor, a constant (maximum) voltage of 12 volts and current of 1,25 Ampere would remain on the heating elements after switching on. These would eventually burn out, because the supplied current continues to cause heating. By adding a PTC resistor in the positive wire, overload can be prevented. This resistor monitors the temperature of the heating element. If the mirror depletion is switched on in the winter period, the PTC resistor will not function in the beginning. The temperature is then too low. The full 12v / 1,25A now flows through the heating elements, causing the mirror glass to heat up quickly in the beginning. (The moisture will then disappear from the mirror glass as quickly as possible).
As the temperature rises, the resistance increases (see the figure below). When the mirror glass has reached a temperature of 20 degrees, the PTC will have a resistance value of 20 ohms. The current has now decreased from 1,25A to 0,6A. This can be calculated with the Ohm's Law:
I=U/R
I = 12 / 20
I = 0,6A
The current intensity has now been halved, which ensures that the mirror glass heats up less quickly. If the temperature of the glass rises to 40 degrees, the PTC has a resistance value of 40 ohms. The current has now dropped to 0,3A.
At a maximum temperature of 60 degrees Celsius, the resistance of the PTC resistor will be 60 Ohms. The current is now only 0,18A. The heating power is now constant and will not increase further due to the low current. The temperature of the mirror glass now also remains constant and cannot overheat. The above values are made up and serve purely as an example to make it as clear as possible. Each manufacturer will use its own amperage (and thus resistance values) for their mirror heaters.
There are also other components in the car that have a PTC resistor, such as a window control motor. If the window mechanism is very heavy (due to a high mechanical load) or the window is opened and closed many times in succession, the temperature of the window operation motor rises. This electric motor is also monitored by a PTC resistor. When the temperature gets too high, this signal is sent to a control unit via the PTC resistor. This temporarily cuts off the power to the motor until the temperature has dropped. This is purely for security to prevent overheating
NTC resistance:
An NTC resistor is a resistor with a Negative Temperature Coefficient. These resistors are applied as temperature sensors of, among other things, the coolant and the intake air. As the temperature increases, the resistance decreases (see picture). Often a constant voltage between 1 and 5 Volt is applied to the sensor. At a low temperature, the resistance value will be high, so the voltage will be low. As the temperature rises, the resistance falls and the voltage rises.
The voltage rise is controlled by the control unit for the characteristics, which determines, among other things, the injection quantity of the injectors. The value can also be passed on to the coolant temperature gauge on the dashboard, or the outside air temperature in the climate control display.
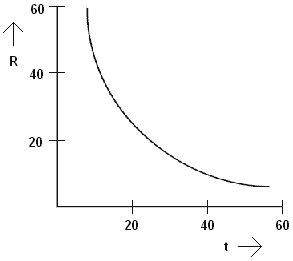
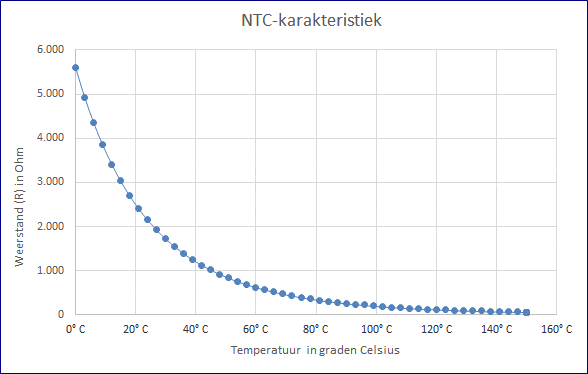
The relationship between resistance and temperature does not have a linear relationship with an NTC resistance. That is, the resistance does not decrease proportionally with the increase in temperature. This can be seen in the figure by the curved line. This line is called a “characteristic” and is logarithmic.
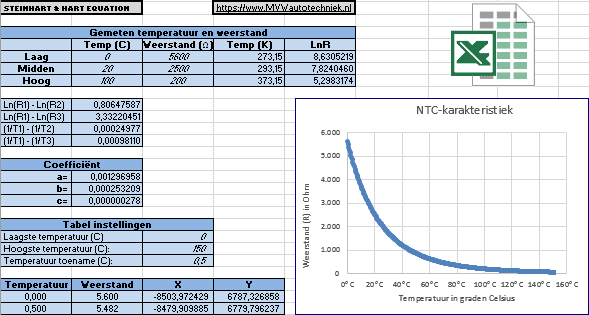
Determining the NTC characteristic:
The NTC characteristic can be partially sketched by determining the corresponding resistance value at three temperatures. For this, the temperature sensor can be measured with an Ohm meter while it is hanging in a heated kettle.
Points can be drawn at different temperatures and resistance values. Lines can be drawn between these points (see image below). In principle, this makes it possible to estimate how the characteristic will develop below 20 and above 100 degrees Celsius.
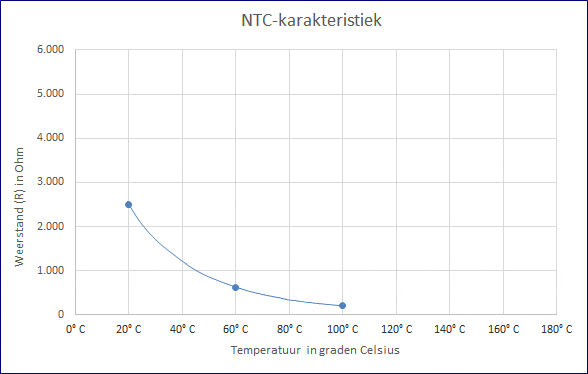
It is interesting to go deeper into this. With the three measured resistance values, the exact resistance can be determined by means of the Steinhart-Hart equation at an infinitely large temperature range. Also, the characteristic can be accurately determined. An Excel file can be downloaded at the bottom of this page with which the characteristic can be formed.
The Steinhart-Hart equation reads:
- T is the temperature in Kelvin;
- R is the resistance at T in Ohms;
- A, B and C are the Steinhart-Hart coefficients that depend on the resistance values at a given temperature.
To find the resistance of a semiconductor at a given temperature, the inverse (R) of the Steinhart-Hart equation must be used. This equation reads as follows:
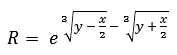
where x and y are determined by the following formulas:
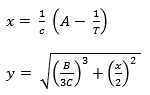
To find the A, B and C coefficients of the Steinhart-Hart, three resistance values (R1, R2 and R3) at a temperature (T1, T2 and T3) must be determined. These should be looked up in the specifications of the semiconductor or measured with a thermometer and an Ohm meter. L1, L2, and R3 are calculated by determining the inverse of the resistance values. Y1, Y2, and Y3 are determined by calculating the temperature in Kelvin to the -1 power.
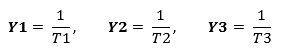
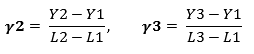
Then the Steinhart-Hart coefficients (A, B and C) can be calculated:
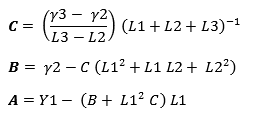
Filling in these coefficients and the ln (R) gives the correct temperature. When the above formulas are filled in, it gives:
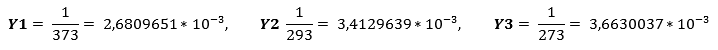
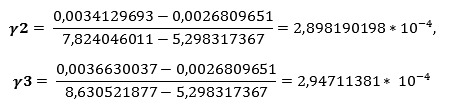

Filling in all the data in the Steinhart-Hart equation:
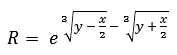
gives:

The desired temperature can be changed by the variable “T”. The calculation will show that at a T of 120 degrees Celsius the resistance is 122 Ohm.
The formula can be filled in with the three previously measured temperatures with which the characteristic can be drawn:
- 2500 Ohms at 20°C;
- 626 Ohms at 60°C;
- 200 Ohms at 100°C.
Related page: