Subjects:
- Exit in the bend
- Calculating the angles sent in
Exit in the bend:
The front wheels do not steer at the same angle when cornering. The inner wheel will always make a “sharper” turn than the outer wheel. The image shows why this is the case.
In the picture you can see that the lines from the front wheels end in the corner M. The corner M is the common pivot point of both front wheels. If the wheels were to rotate at the same angle (the wheels are then both in exactly the same position), the lines from the wheels would also run parallel to each other to infinity. They never find the common pivot point M. Therefore, the steering characteristics will be very poor in this situation. This whole principle is called “toe out in the bend”. All modern cars are constructed with this characteristic.
On slippery surfaces, e.g. the floor in the parking garage, a squeak of the tires can be heard when turning. That's because of this principle. The inner wheel, which is at a sharper angle than the outer, will experience some form of slip. This is called a steering error. More information about the steering error (and a graph) can be found on the page steering error.
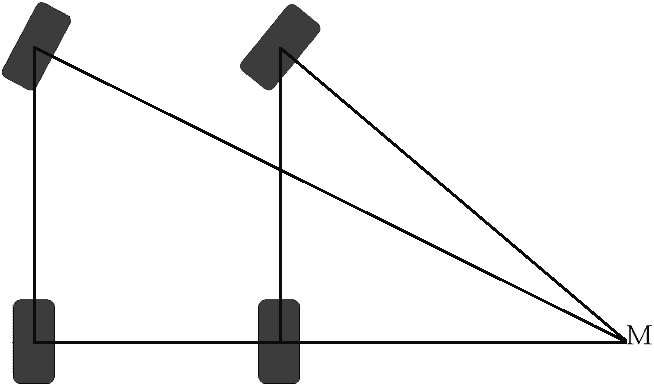
This page explains how to calculate the steered angles (in degrees) of both front wheels using a number of data.
Calculating the angles sent in:
The following data is required from the vehicle to calculate the angles turned in:
- track width
- Wheelbase
- Turning circle diameter
- Knuckle spacing (on this page we keep the knuckle spacing equal to the track width)
- Tire size (depending on calculation. On this page the tire size is calculated, but it is also possible to calculate up to the bumper corners. However, more corners will be added).
| Track width = 1600mm | Wheelbase = 3200mm |
| Diameter turning circle = 13,225m | Knuckle spacing = Track width = 1600mm |
| Tire size = 225 | L and L' = unknown |
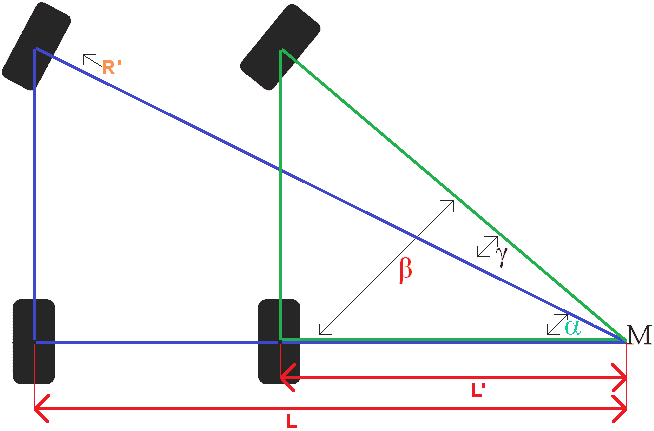
Explanation of the symbols:
α = Alpha
β = Beta
γ = Gamma
These letters are from the Greek alphabet and are often used for calculations in angles.
L = the length
L' = L with “accent” as an addition, which is often used mathematically. It might as well have been L2. For example, a 3rd L had been given two accents: L”.
The same goes for R”.
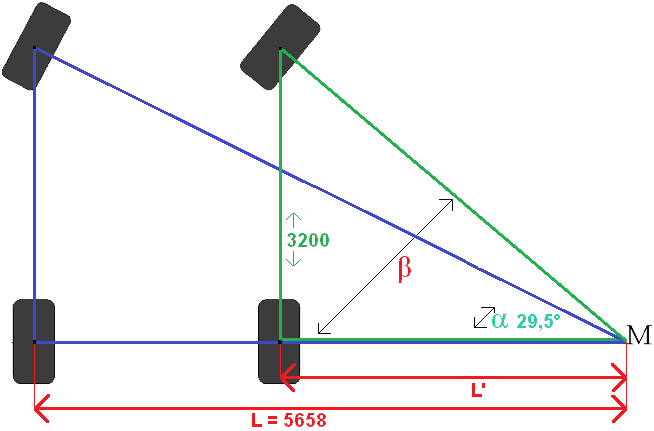
The angles Alpha, Beta and Gamma lie at point M.
Angle Alpha + Gamma = Angle Beta.
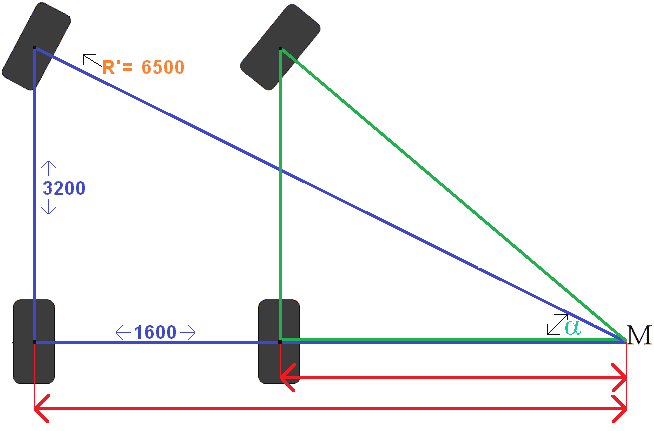
The entire turning circle is 13,225 meters. R is the radius, so that's the half turning circle (6612,5). In the picture R' is given. This R' is not a fixed fact. This must be calculated by subtracting half of the bandwidth. Another way is to subtract the stub axle distance, but on this page we will stick to: Track width = stub axle distance. From this follows the simple calculation:
R = 6612,5 mm
R' = R – half bandwidth
R' = 6612,5 – (225 : 2)
R' = 6612,5 – 112,5
R' = 6500 mm
We fill in the R' in the image. Next, we calculate the angle sin α (sine Alpha) using the Sine rule. Then we calculate the other angles with the Tangent and the Pythagorean Theorem.
Angle calculation with the Sine:
Sin α = Opposite side : Bevel side
Sin α = Wb : R'
Sin α = 3200 : 6500
Sin α = 0.492
Inv Sin α = 29,5°
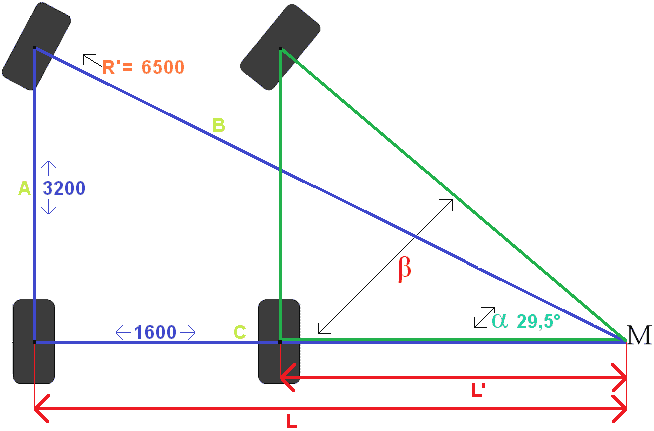
Explanation of the calculation:
We want to calculate Sin α. The sine is dividing the opposite side by the hypotenuse (memory: SIN = SOS).
Wb= wheelbase = 3200mm. We previously calculated R' = 6500mm.
Then we divide that by each other; then we have Sin α = 0.492. To convert this number to an angle, press the sin-1 button in the calculator (usually pressing the Shift key first and then the Sin key) followed by 0.492, or the ANS button. Now the angle of 29,5 degrees comes into view.
Sin α is now known. Now we actually want to calculate tan β, but then we need the length L'. This must be calculated first. So we use the answer of the calculation L' to calculate Tan β later on.
L' = L – Track width.
We calculate L using the Pythagorean theorem. The 2 sides of the triangle are known (6500 and 3200). The other side of 1600 is the track width that runs from tire to tire, so that doesn't count. We are going to calculate the bottom side, which runs from the left rear tire to the common point M. The calculation is therefore about the complete blue triangle.
The Pythagorean theorem looks like this:
A^2 + B^2 = C^2. (The sign ^ is a symbol for “power”. So it says A squared + B squared = C squared. We formulate it differently here.
The length 3200 we call A, 6500 we call B and the lower unknown side we call C:
C^2 = 6500^2 – 3200^2
C^2 = 42250000 – 10240000
C^2 = 32010000^2
To get rid of the square, let's take the square root of the number.
C^2 = √32010000
C = 5658mm.
Side C is actually length L.
Now L' can be calculated. The full length L and the track width are known, so the two can easily be subtracted from each other:
L' = L – Track width
L' = 5658 – 1600
L' = 4058mm
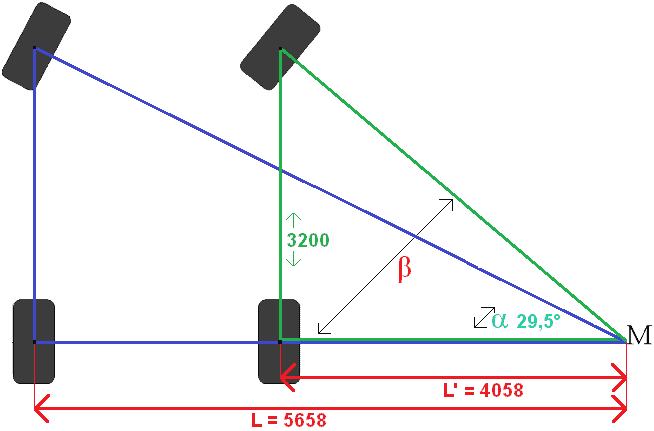
Now the Wb and L' are known. Two of the three sides of the triangle are known, so with the Tangent the third side can be Worden calculated:
Angle calculation with the Tangent:
Tan β = Opposite side : Adjacent side
Tan β = Wb : L'
Tan β = 3200 : 4058
Tan = 0.789
Inv Tan β = 38,3°
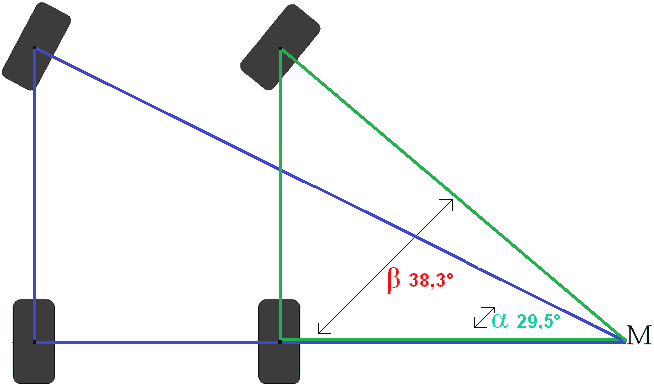
Explanation of the calculation:
We want to calculate Tan β. The tangent is dividing the opposite side by the adjacent side (memory: TAN = TOA).
Wb= wheelbase = 3200mm. We previously calculated L' = 4058mm.
Then we divide that by each other; then we have Tan β = 0.789. To convert this number to an angle, enter the tan-1 button in the calculator (usually pressing the Shift button first and then the Tan button) followed by 0.789, or the ANS button. Now the angle of 38,3 degrees comes into view.
Now steered angles of both front wheels have been calculated. The left front wheel is at an angle of 29,5° and the right front wheel at an angle of 38,3°. This means that the steered angle has a difference in both wheels of 8,8°. In a left turn, the same steering angle will result with the same steering angle.
On the page wheel geometry several wheel positions are described.
