Subjects:
- Hydraulic cylinder
- Calculate stroke volume
- Calculate system pressure
- Calculate volumetric flow
- Calculate power
Hydraulic cylinder:
A hydraulic cylinder consists of a housing containing a piston and piston rod. The operation is based on Pascal's Law, which has already been described. The hydraulic fluid is pumped into the cylinder on one side, causing the piston to move in a straight line. Very high forces can be transmitted with the hydraulic cylinder. The following figure shows the three situations of a double-acting cylinder:
- A: The piston with the piston rod are in the leftmost position.
- B: hydraulic fluid is supplied via the left connection of the cylinder. The fluid pushes the piston to the right. The liquid located on the right side of the piston is discharged from the cylinder via the right connection.
- C: the piston is in the rightmost position.
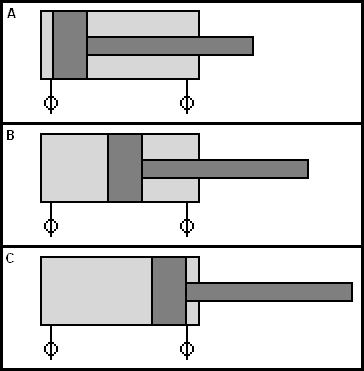
On the side of the piston rod (right side in the picture above), the area where the hydraulic fluid presses against the piston is smaller.
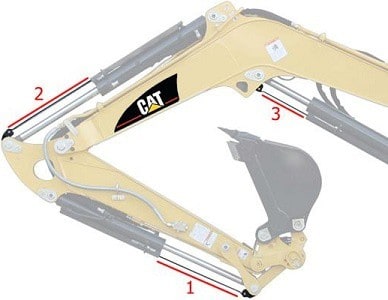
The following figure shows the mechanism of an excavator. The combination of hinges, levers and separately operable hydraulic cylinders ensures that the bucket is very manoeuvrable. The cylinders are of the double-acting type: by changing the fluid direction to and from the cylinder, the piston moves in the opposite direction.
In addition to the double-acting cylinders, there are also:
- Single-acting cylinder: This type of cylinder contains one hydraulic connection. A spring behind the piston provides the return stroke.
- Cylinder with hydraulic buffering: the piston movement is braked at the end of the stroke.
- Telescopic cylinder: a number of cylinders pushed together create a large working length when extending. When retracted, the installation space is relatively small, thanks to the telescopic version.
Calculate stroke volume:
Due to the different designs of cylinders, their applications are versatile: when the piston rod has to exert a lot of force, the diameter of the piston rod is larger, as well as the piston, cylinder and the volume of liquid in the cylinder. The dimensions depend on the installation location and the application for which the cylinder is used. We come across the following dimensions:
- piston diameter (D)
- rod diameter (d)
- stroke of the piston(s)
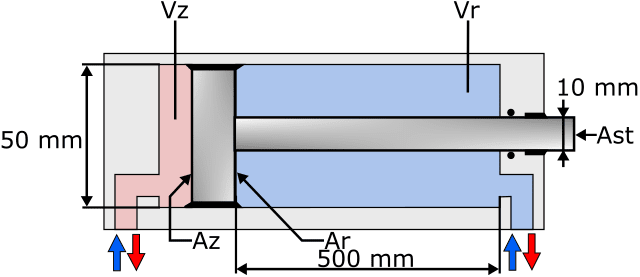
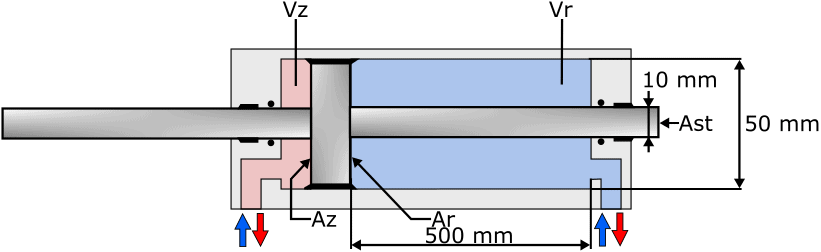
The image below shows a cylinder containing the piston with piston rod. The explanation of the abbreviations is shown next to the image.
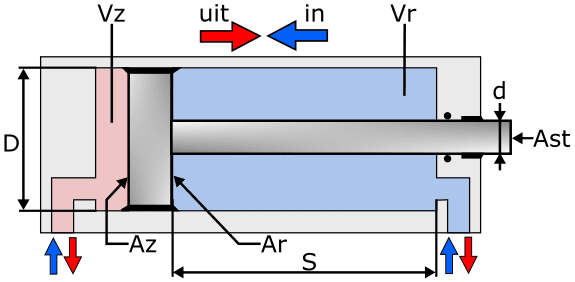
Declaration:
- D = piston diameter
- d = rod diameter
- s = stroke
- Az = piston surface
- Ar = ring area
- Ast = rod area
- Vz = volume piston side
- Vr = rod side volume
With the dimensions of the piston and cylinder we can calculate the swept volume on the piston side (Vz). For that we need the area of the piston (Az) and multiply this number by the stroke. When Az is unknown, we can calculate the area with the following formula:
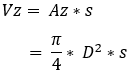
To determine the stroke formula on the right side of the piston, we need to subtract the area of the piston rod. The following formula arises:
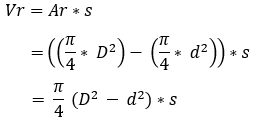
With these formulas we are going to calculate the swept volume of the cylinder below.
The data to calculate the swept volume on the piston side when fully extended is entered into the formula. The final answer is in cubic meters because it is a volume. We convert the last answer into scientific notation.
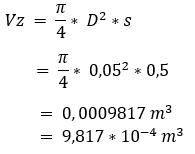
Then we fill in the data on the rod side to calculate what the volume of fluid is there when the piston is fully retracted. We end up with a lower liquid volume, because this space is occupied by the piston rod. We also convert this answer into scientific notation.
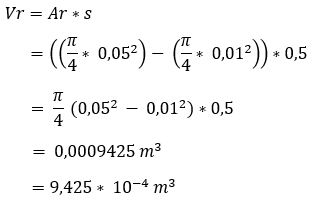
For cylinders with a continuous piston rod with the same diameters, it is easier to determine the liquid flow: the incoming volume flow is equal to the outgoing volume.
To calculate system pressure:
The pressure in the cylinder to push the piston to the right prevails on the piston surface Az. We can calculate this pressure if we know the force exerted by the piston on the object to be moved. This force is 10 kN (10.000 N). For convenience, we use the remaining piston and cylinder data from the previous section.
We use the following formula to calculate the pressure in the cylinder. The force F is known (10.000 N), but the surface of the piston is still unknown.

So we first calculate the surface of the piston:
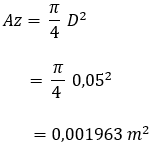
Now that we know the area of the piston, we can calculate the pressure:
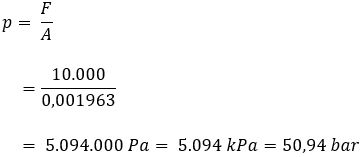
Dividing F (Newton) by A (square meter) we get an answer in Newtons per square meter [N/m²]. This is equal to Pascal, because 1 Pa = 1 N/m².
By dividing the number of Pascals by 100.000 we obtain the number of bars. This is reflected in the answer of the above formula.
Calculate volumetric flow:
We can calculate the volumetric flow by dividing the already known data by the time in which the piston makes the full stroke(s). We set this time (t) at 5 seconds.
We calculate the volumetric flow with the following formula:

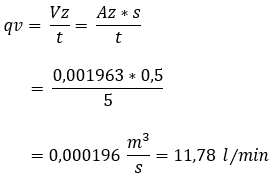
Calculate power:
Finally, we can calculate the power required to move the cylinder from left to right. To do this, we multiply the system pressure by the volume flow. The calculation is shown below.
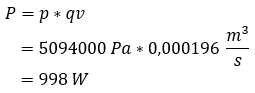
Related page:
