Subjects:
- Pressure in a hydraulic system
Pressure in a hydraulic system:
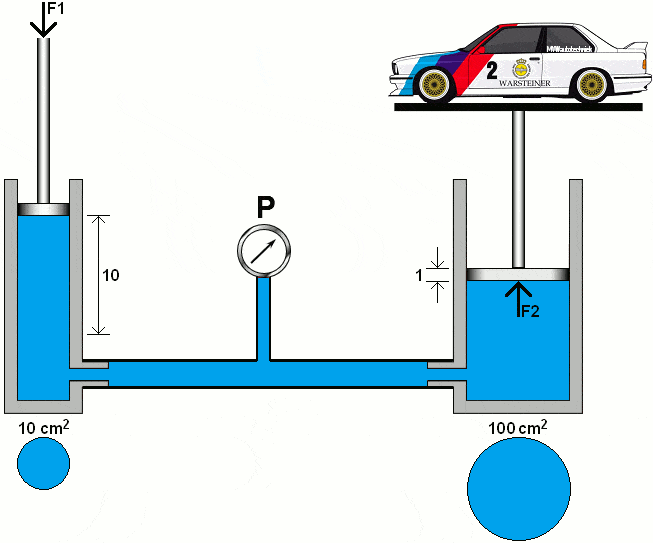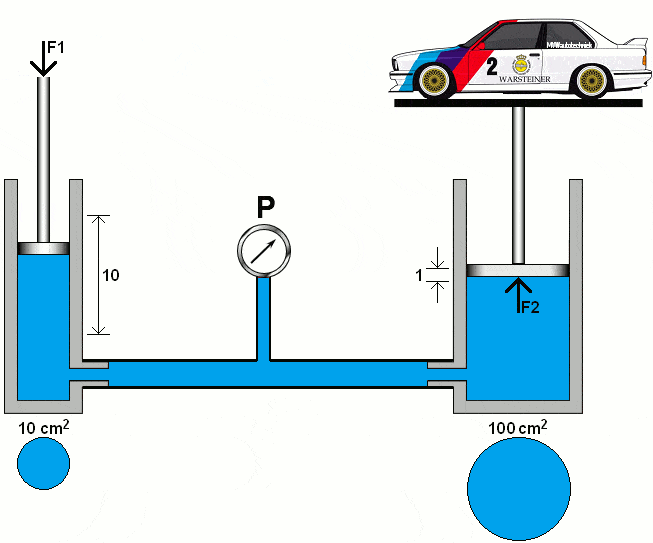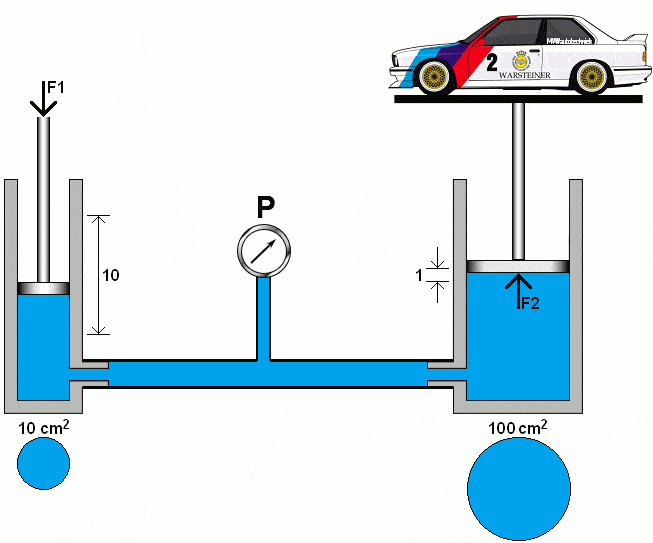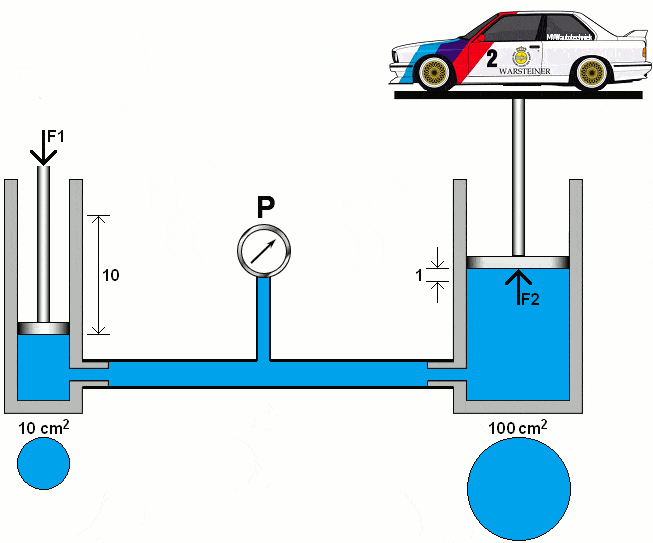
Hydraulic systems work according to the laws of hydrostatics. Pascal's Law states: "The pressure in a compressed fluid at rest propagate uniformly in all directions in a closed system."
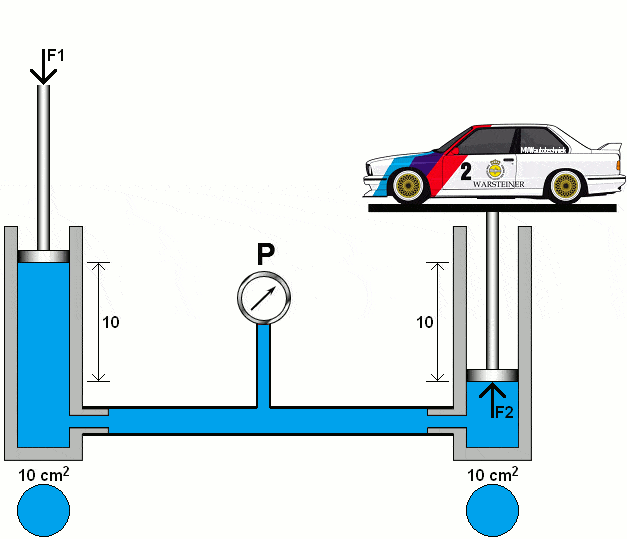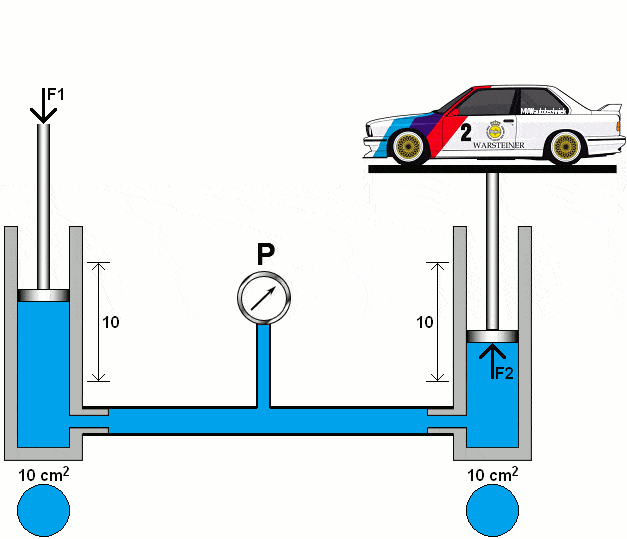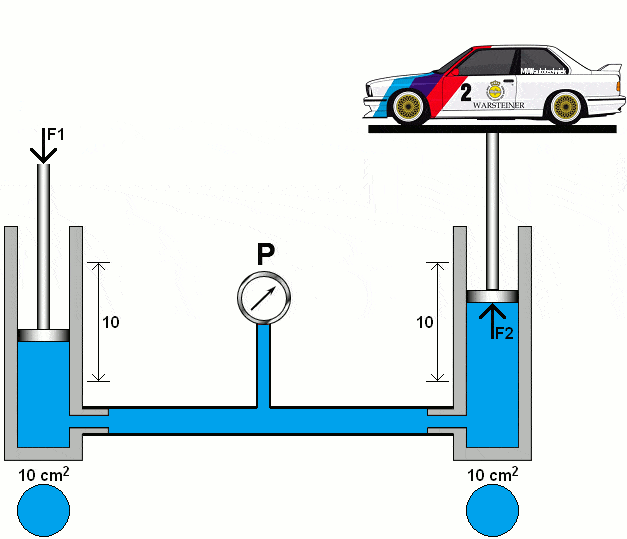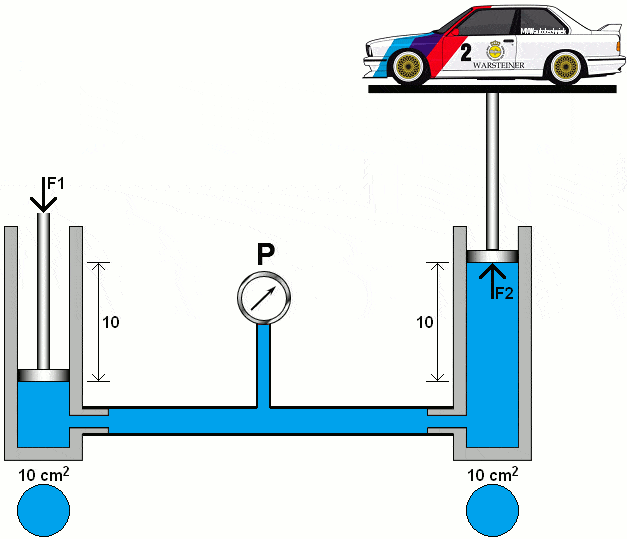
The following animation shows the principle of a hydraulic system with two pistons, pipes with a pressure gauge and oil (colored blue).
The left piston is pushed downwards with a certain force (F1). Due to the fluid displacement in the left piston, the right piston is pushed upwards with the force (F2). The diameters of both cylinders are the same. In this section we will calculate the pressures and forces in two hydraulic systems.
To calculate the force F2, we first need to find out the weight (kg) and the gravitational acceleration (m/s²). The weight of the fictitious BMW is 1000 kg. We round the gravitational acceleration to 10. With that data we fill in the formula to calculate the required force:
The following formula can calculate the pressure indicated by the pressure gauge:
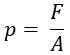
Whereby:
- p = pressure in Pa (Pascals)
- F = force in N (Newtons)
- A = area in m²
We fill in the formula to calculate the fluid pressure under both pistons.
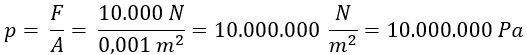
A mnemonic:
- 1 kPa (kilopascals) = 1.000 Pa;
- 1 MPa (megapascals) = 1.000.000 Pa;
- 1 bar = 100.000 Pa = 100.000 N/cm².
A pressure of 10.000.000 Pa is therefore equal to 100 bar.
In the following animation, the diameter of the right piston has increased tenfold. We calculate the pressure under the right piston with the area (A2) of 100 cm².
The fluid pressure in the entire system is the same. We enter the pressure in the following formulas:
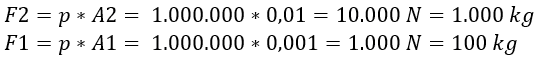
The formulas show that the 1000 kg car can be lifted with a force (F1) on the left piston of 100 kg. The distance covered by the left piston is proportionally ten times greater than that of the right piston.
We can show that the pressure in the entire system is equal by filling in the following equation:
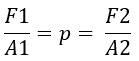
Related page:
