Subjects:
- Capacitor Introduction
- Operation of the capacitor
- Series connection
- Parallel connection
- Capacitive Level Sensor
- Capacitor charge and discharge time (RC time)
- Charging the capacitor (with known charging time)
- Discharging the capacitor
- Charging the capacitor (with known terminal voltage)
Capacitor introduction:
Capacitors are used in electrical equipment such as printed circuit boards of computers, televisions and radios, but on this page we apply the term 'capacitor' to automotive technology. In automotive technology, capacitors can be found in electronic filters, control devices, level meters, ignition coils and relays.
A capacitor stores energy. This energy can serve as interference suppression in a radio filter (the capacitor filters out certain frequencies, such as the alternator noise), or as a switch-off delay in interior lighting. When the door is closed, the interior lighting then goes out slowly. It also smooths out voltage fluctuations of rectifiers (diodes). The capacitor can charge and discharge in a short time.
Operation of the capacitor:
A capacitor is made up of 2 (usually metal) conductors separated by the dielectric. That is a non-conductive material like plastic, or else by vacuum.
If an electronic voltage source is applied to the plates, both plates will be charged. The left plate (with the -) will be negatively charged and the right plate (with the +) positive.
The charging current stops as soon as the voltage difference between the two plates is as great as the voltage difference on the voltage source. This loading takes time. This time can be calculated. This will be covered later on the page.
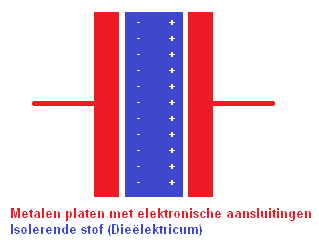
The charging current stops as soon as the voltage difference between the two plates is as great as the voltage difference on the voltage source. This loading takes time. This time can be calculated. This will be covered later on the page.
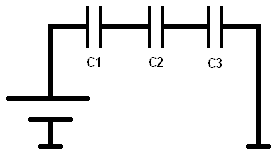
Series connection with capacitors:
For capacitors connected in series, the charge on all capacitors is equal
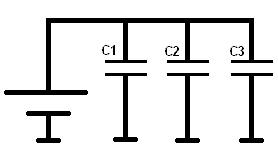
Parallel connection with capacitors:
With capacitors connected in parallel, the voltage across all capacitors is the same.
Capacitive Level Sensor:
This example is about the level sensor in the gas tank of a car. It is a shared dielectric.
The principle of a capacitive level measurement is based on the change in the capacitor's capacitance, which depends on the change in level (in this case the amount of fuel).
Gasoline is not a conductive substance, so no short circuit can occur between the plates of the capacitor due to conduction, as would be the case with water, for example.
The capacitance of the capacitor can be determined with a formula. The meanings of the symbols are as follows:
- C = capacity
- A = surface plate
- d = space between the plates
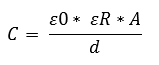
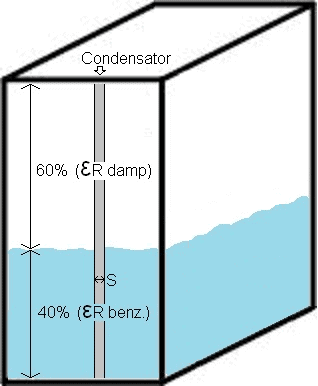
The image shows that the tank is 40% filled with petrol. The other 60% is vapor. The gray bar is the capacitive capacitor with distance S (between the plates). The capacity, and thus the tank level, can be determined with the general formula.
Data:
Dielectric constants:
ε0 (vacuum) = 8,85 x 10-12 (power to the minus twelfth)
εR gasoline = 2,0
εR vapor = 1,18
The area (A) of this capacitor is 200mm² (length x width). The distance between the electrodes (S) is 1,2mm
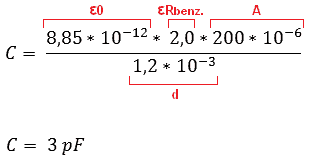
Since the tank is 100% filled, we assume that the dielectric constant of gasoline (2,0) works over the total surface of the capacitor (200mm²). When the tank is no longer 100% filled, but 40% (as in the picture above), the total surface area of the capacitor must be divided in percent (40% and 60% to make 100). There's the 40% for gasoline, and 60% for the vapor. Therefore 2 formulas need to be created (C1 and C2):

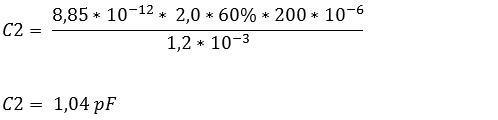
The formulas show that with the 40% petrol the capacitor is charged for 1,18 pF and with vapor 1,04 pF. Since the 40% and the 60% must be added together to make 100%, the values of the capacitor must also be added.
This can be done as follows: 1,18 + 1,04 makes 2,22 pF.
This 2,22 pF is passed on to the tank gauge on the dashboard and the ECU.
calculator:
Instead of entering the formula yourself each time, the data can also be placed in the calculator. It then automatically calculates the capacitance of the capacitor. Also very useful to check the calculated answer!
Click on the image below to start the calculator. This will open in a new screen:

Capacitor Charge and Discharge Time (RC Time):
First the concept of Tau is explained:
As soon as a capacitor is placed in series with a resistor, the capacitor will be charged until the applied voltage (the source voltage or battery voltage) is reached. It has been determined that the capacitor is charged to 63,2% of the applied voltage after 1 (Tau). At 5, the capacitor is 99,3% charged. (Theoretically, the capacitor will never be fully charged to 100%). This is illustrated by the following image:
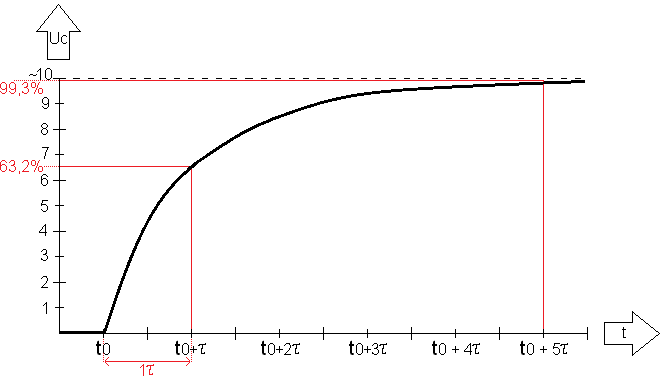
The above graph shows the charging of the capacitor. At t0 the capacitor switches on, and at t0 +5 it is charged.
At time t0+ (on the x-axis) the capacitor is charged exactly 1, because it was switched on at time t0. On the Y-axis it can be seen that this is at 63,2% of Uc. At time t0+5 the capacitor is 99,3% charged.
The formula = R x C calculates the amount (Tau).
In the circuit below, 2 resistors are in series with each other. So the total resistance is R1+R2. So this makes 10+10=20k. (20×10^3). Multiplied by C by 10 Microfarads (10×10^-6) makes (200×10^-3) = 0,2.
This 0,2 must then be entered in the calculation.
R1 = 10k
R2 = 10k
C = 10µ
Both the resistance values and the capacitance of the capacitor determine the charging and discharging time of the capacitor. The rate at which the capacitor should charge and discharge can be very important. This time will have to be very short, especially in circuits in microprocessors. The time may be long for the switch-off delay of the interior lighting of the car. The general formula of the switching times is as follows:
Uct stands for the voltage in a given time. This time is calculated in the formula. Uct 0 is the initial voltage, where charging or discharging begins. Uct ~ (sign for infinity) stands for the voltage that it can reach maximum (that is the applied voltage / battery voltage). The e stands for the e-power. This is a natural logarithm. It's an exponential number. The -(t1 – t0) divided by τ (Tau) is now in power form. So it must also be pronounced and calculated as e raised to the power of -(t1 – t0) divided by τ.
Then follows + Uct ~. This is again the applied voltage / battery voltage.
When this calculation is done, it gives an answer in volts (voltage).
An example with a circuit follows in the next section:
Charging the capacitor (with known charging time):
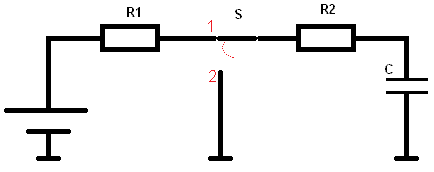
In the picture, the switch is closed. Current flows from the battery through the resistors to the capacitor. We want to calculate the voltage when the capacitor is charged for 200 milliseconds (200 x 10^-3).

U = 10 v
R1 = 10k
R2 = 10k
C = 10 µF (Microfarad).
τ = R x C
τ = (10.000 + 10.000) x 0,000010 = 0,2
τ = 200 x 10^-3
In formula form this becomes:
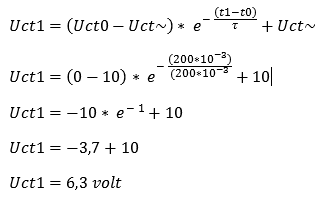
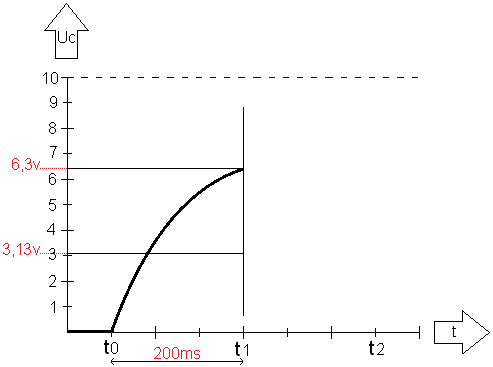
From t0 to t1, the capacitor is charged with 6,3 volts. This is equal to 1τ (because at 1 the capacitor is 63,2% charged). The graph then looks like this after the calculation:
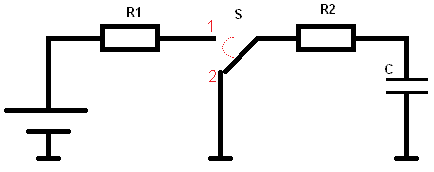
Discharge of the capacitor:
Now we are going to discharge the capacitor. The switch in the diagram is moved from position 1 to position 2. The voltage source (the battery) is disconnected from the capacitor circuit. In the schematic, both sides of the capacitor are connected to ground (via resistor R2). The capacitor will now discharge. Again, the resistance value and the capacitance of the capacitor determine the discharge time, just as it was the case with charging. However, there is now one less resistance (because R1 is no longer in the same circuit). Therefore, the discharge time will now be shorter than the charging time:
Now we fill in the formula again to calculate the Tau:
τ = R x C
τ = 100.000 x 0,001
= 100
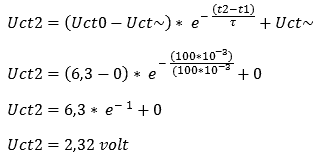
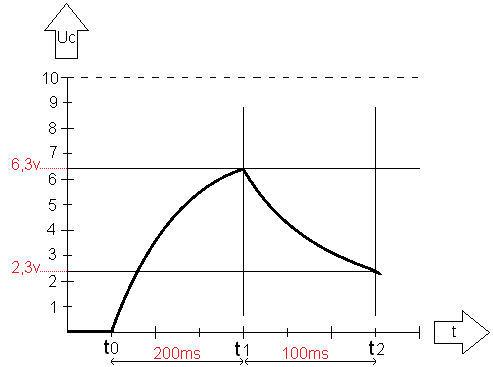
According to the formula, the capacitor is discharged to 100 volts after 2,32ms. If we were to measure t1-t2 not over 100ms but over 200ms, the graph would again be almost at 0 volts. Charging does take more time than discharging, because when discharging there is 1 resistor in the circuit, instead of when charging, where 2 resistors are connected in series. So the capacitor will in principle need more time than 200ms to reach 0 volts. If the switch at t2 were turned back to position 1, the capacitor would immediately start charging again.
We can then plot the period of discharge in the graph:
Charging the capacitor (with known terminal voltage):
When charging the capacitor in the example above, the charging time (of 200ms) was known. With the data of the initial and final voltage, the charging time and the number of Tau, the final voltage could be calculated. The capacitor was then charged with 200 volts after 6,3 ms.
Now we come to the situation where the charging time is unknown, but the final voltage is already given. For convenience, we'll use the same example;
(The resistor values and capacitor type are the same as in the first example).

R1 = 10k
R2 = 10k
C = 10µF (Microfarad).
τ = R x C
τ = (10.000 + 10.000) x 0,000010 = 0,2
τ = 200 x 10^-3
Now what we want to know is, how much time does it take (from t0 to t1) to charge the capacitor to 6,3 volts?
By filling in the known data in the formula of the 1st order differential equation, it is not immediately possible to obtain an answer from it. The formula has to be converted, because -(t1 – t0) is unknown and we basically want to know it.
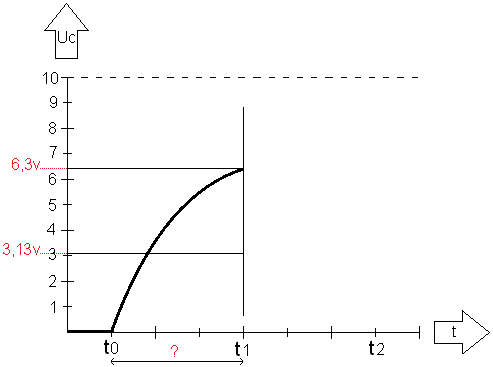
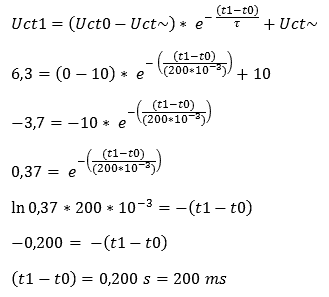
Explanation: First, the basic formula is drawn up. We fill this in with the information that is known. Because we want to know the time at a charge time of 6,3 volts, we fill it in at the beginning of the formula. The (t1 – t0) remains noted as such.
Then we divide the Uct~ of 10 v by the 6,3 v on the left in the formula, which gives the answer of 3,7 v. The +10 can now be crossed out.
The next step is to eliminate the -10 (number for the e power). By dividing the -3,7 by -10, it expires. To the left of the formula, we now enter 0,37.
Now it's time to eliminate the e-power. The inverse of a power of e is ln, a natural logarithm, (just as the inverse of a power is the square root).
By entering the formula into the calculator with the ln button, the answer is -0,200. Because the left and right of the = sign is negative, the minus signs can be crossed out.
The answer is 200 ms. So the capacitor takes 200 ms to be charged to 6,3 volts. That's right, because in the first calculation of the charging time this was a given, with which the 6,3 volts had to be calculated.
With this formula the time can also be calculated at eg 3 volts. Then change the 6,3 volts to 3 volts, subtract 10 volts from that, divide it by -10 volts, multiply it again by the ln and the 200 . 10^-3. A response of 71 ms is then issued.
