Subjects:
- Preface
- Wheatstone Bridge in Balance
- Wheatstone unbalanced bridge (resistance values known)
- Wheatstone Bridge with unknown resistance value
Preface:
Wheatstone's bridge is an electrical bridge circuit for accurately measuring a constant or changing electrical resistance. This circuit can be used to measure physical quantities such as temperature and pressure, as we see in the air mass meter (temperature of the hot wire) and MAP sensor (pressure in the intake manifold).
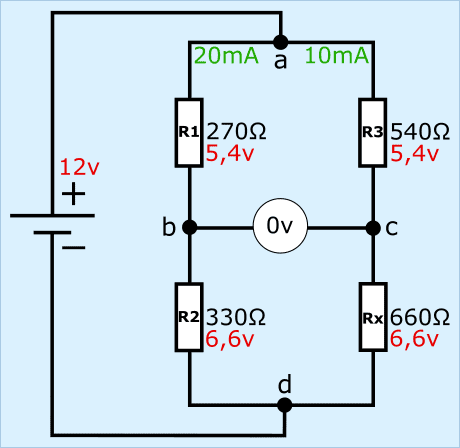
There are four in Wheatstone's bridge resistors, of which three with a known, and one with an unknown resistance. This means that the bridge actually consists of two voltage dividers that are connected in parallel.
In the picture we see the resistors R1 to R3 (known resistance values) and Rx (unknown), with a voltmeter in the middle of the two voltage dividers and a voltage source to the left of the bridge.
Wheatstone's bridge is balanced or balanced if the output voltage between points b and c equals 0 volts. Different situations are shown in the following paragraphs.
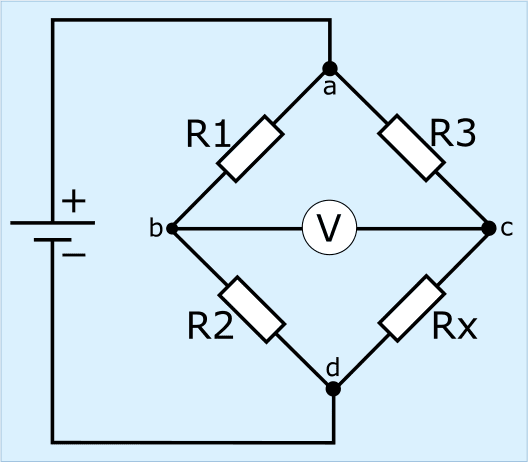
Balanced Wheatstone Bridge:
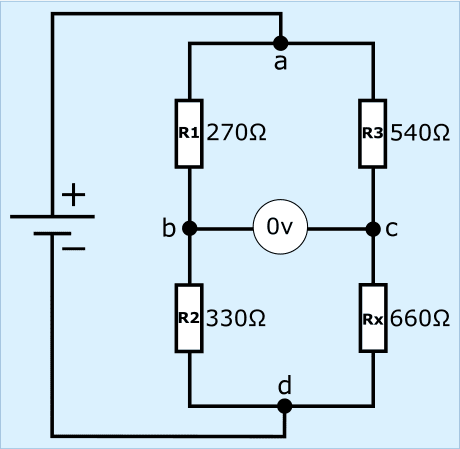
The Wheatstone bridge is balanced or in equilibrium if the output voltage is equal to 0 volts, because the resistance values left and right are proportional to each other.
The circuit in this section is drawn differently than in the previous section, but is based on the same operation.
- the resistors R1 and R2 have a resistance of 270 and 330 Ω. Added together, this is 600 ;
- the resistors R3 and Rx have a resistance of 540 and 660 Ω. Added together, this is 1200 Ω.
The ratios between the resistors left and right are equal to each other. Thus, the resistance ratios and voltage drops are equal to each other between R1 and R3, as well as R2 and Rx.
In the formulas below, the equal resistance ratios and voltage drops are shown:
![]() en
en ![]()
With a known supply voltage and resistance values, we can determine the voltage drops across the resistors, and thus the voltage difference between points b and c. In the example below, we calculate the voltage difference between points b and c in a balanced Wheatstone bridge. The knowledge of the Ohm's law and calculate with series & parallel connections is a requirement.
1. calculate the currents through resistors R1 and R2 (RV = Replacement Resistance):
![]()
2. calculate the voltage drop across resistors R1 and R2:
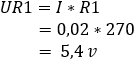
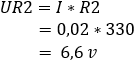
3. calculate the currents through the resistors R1 and R2:![]()
4. calculate the voltage drop across resistors R3 and Rx:
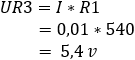
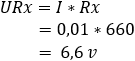
The voltage at points b and c is 5,4 volts. The potential difference is equal to 0 volts.
Wheatstone unbalanced bridge (resistance values known):
Due to a resistance change of Rx, the Wheatstone bridge will become unbalanced. The resistance change can occur due to, for example, a changing temperature, where Rx is a thermistor is. The voltage divider between R1 and R2 will remain the same, but not between R3 and Rx. Because there the voltage divider changes, we get a different voltage at point c. In this example, the resistance value of Rx has dropped from 600 to 460 Ω.
1. calculate the currents through resistors R1 and R2:
![]()
2. calculate the voltage drop across resistors R1 and R2:
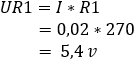
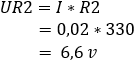
4. calculate the voltage drop across resistors R3 and Rx:
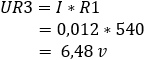
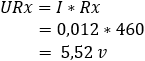
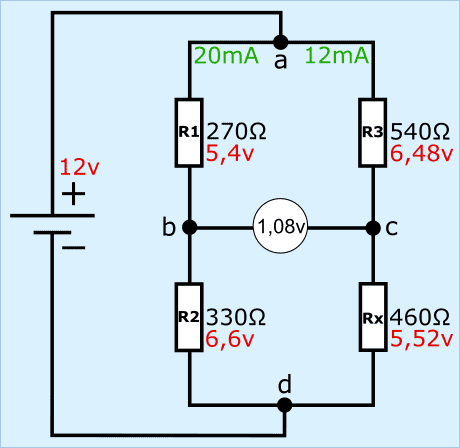
In the two examples, the resistance value of Rx has changed from 660 to 460 Ω. Due to this resistance change, the voltage between bc has changed from 0 volts to 1,08 volts. When this bridge from Wheatstone is built into the sensor electronics, the voltage of 1,08 volts is seen as the signal voltage. This signal voltage is sent to the ECU via a signal wire. The A/D converter in the ECU converts the analog voltage into a digital message, which can be read by the microprocessor.
Wheatstone bridge with unknown resistance value:
In the previous sections, we assumed a known resistance value of Rx. Since this resistance value is variable, we can take it a step further by calculating this resistance value to balance Wheatstone's bridge.
In this circuit, R1 and R2 are again 270 and 330 . The resistance of R3 has been lowered to 100 Ω and Rx is unknown. If, in addition to the resistance value, the voltages and currents are also unknown, we can calculate the resistance value Rx in two ways:
Way 1:
1. we first look at the general formula and then fill in the resistance values:
![]() ->
-> ![]()
2. Between 270 and 100 is a factor of 2,7, as well as between 330 and the unknown value.
By dividing 330 by 2,7 we arrive at a resistance of 122,2 Ω.
![]()
Way 2:
1. via the general formula in which we crossly multiply the resistances:
![]()
2. we build the formula by taking Rx to the left of = and dividing by R1. We also arrive at the resistance value of 122,2 Ω.
![]()
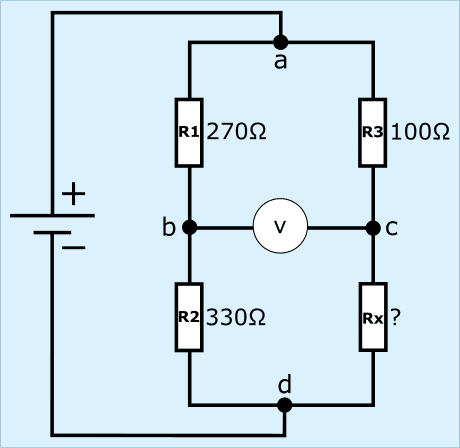
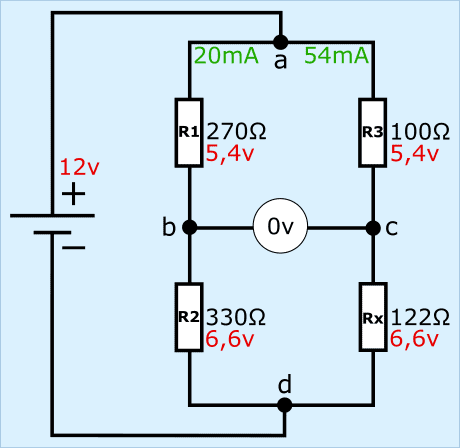
Of course we check whether we have a balanced bridge with the previously calculated resistance of 122 Ω.
The resistors R1 and R2 with the currents and partial voltages are the same as in the examples in paragraphs 1 and 2, so they are considered known. We focus on the right side of the bridge.
1. calculate the current through R3 and Rx:
![]()
2. calculate the voltage drop across resistors R3 and Rx:
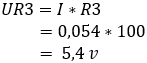
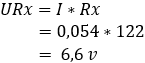
The voltage difference between points b and c is 0 volts because resistors R1 and R3 both absorb 5,4, so the bridge is now balanced.
Related pages:
