Subjects:
- Calculating axle load using VLS
- Calculate front axle load
- Difference Between Weight and Mass
- Calculate rear axle load
- Calculate bullet pressure
- Calculating the influence of the nose weight on the rear axle
Calculating axle load using VLS:
The axle loads of a vehicle can be calculated with a schematic drawing and the data of the car. By means of a VLS (Free Body Scheme) a car with the relevant forces can be drawn (see image below). The conditions of a VLS are that the road surface is not drawn. Even if the vehicle is on a hill, the vehicle may not be drawn obliquely, but a horizontal force with a direction must be drawn in the VLS.
The advantage of working with a VLS is that the unnecessary things are left out. For example, when calculating the internal moments or axle load of a trailer, it is useful to only draw the trailer instead of a car with trailer. By only drawing what is necessary, you avoid making mistakes (by including too many horizontal / vertical forces in the calculation that do not belong in it).
First, the weight must be calculated by means of the gravitational acceleration acting on the vehicle. Gravity depends on where the vehicle is located on Earth. In the Netherlands, the gravitational acceleration is 9,81 m/s.
The vehicle mass must be multiplied by gravity. That gives: 1500 x 9.81 = 14.715N (The unit of force is Newton). It should be mentioned here that the gravitational acceleration is sometimes also called gravitational acceleration, gravitational constant or fall speed. Also, the number 9,81 is sometimes rounded off as 9,8 or very roughly as 10. This is easier to calculate (1500 / 10 is easier to calculate by heart than 1500/ 9.81) but the final answer is certainly not accurate. Therefore always apply the 9,81 m/s, unless it is stated differently in an exam question, for example.
The total force with which the vehicle is pressed onto the road surface is therefore 14.715 Newtons. This force is distributed over both axles of the car.
The axle load is often higher at the front, because that is where the engine is located. This can be seen in the image by the center of gravity, which is at the front when viewed from the center. The center of gravity is an imaginary pivot point. If this center of gravity were exactly in the middle, the axle load on both axles would be the same (divide vehicle mass by 2). Because the distances of the wheels, the location of the center of gravity and the total vehicle mass are known, the axle loads at the front and rear can be calculated.
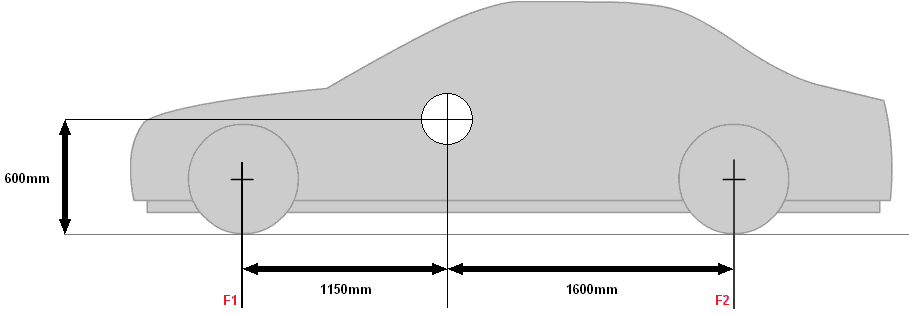
Vehicle mass: 1500kg
Weight: 14715N
Height of road surface – articulation point: 60cm
Distance F1 – articulation point: 115cm
Distance pivot point – F2: 160cm
Distance F1 – F2: 115+160= 275cm (this is the wheelbase)
Calculate axle load F2 (rear axle):
14715 x 1,15 – F2 x 2,75 = 0
16922 – F2 x 2,75 = 0
F2 = 16922 / 2,75
F2 = 6154N
The calculation is detailed below:
- To calculate F1 and F2, one must first be calculated. We choose to calculate F2 first.
We make the pivot at F1. Everything to the right is positive and everything to the left is negative. That means that the forces directed downwards are positive, and the force F2 upwards is negative. We fill in the first part of the formula.
14715 x 1,15 – F2 x 2,75 = 0
(Fill in this last 0 by default, because further in the calculation the numbers to the left and right of the ” = ” sign are swapped) - Force x arm: The weight of 14715 is multiplied by the distance of 1,15:
14715 1,15 x = 16922 - Now we fill it back into the formula:
16922 – F2 x 2,75 = 0 - Move the 16922 to the other side where the 0 is:
F2 x 2,75 = 16922 - Divide both sides by 2,75 to remove it to the left of the = sign:
F2 = 16922 / 2,75 - That results in:
F2 = 6154N.
Difference Between Weight and Mass:
Remember that weight is not the same as mass. The weight of F2 in the previous calculation is 6154 Newtons. A mass is always in kilograms. It must therefore always be divided by the gravitational acceleration of 9,81. (6154 / 9,81 = 627,3kg) Just think of the mass of empty vehicle that is stated on the registration certificate. That is always in kg. To make the above story clear; There is no gravity in space. Everything floats there, no matter how heavy it is. Everything does have a weight; when you throw a carton of milk against something, or a stone, it will have a different impact. The carton of milk will not quickly damage anything when it hits the wall, for example, but the stone will certainly cause damage. This is because the force with which the object comes to a stop is higher with the stone than with the carton of milk. This proves that weight is also present and important in space, but mass is not. The mass is due to the gravitational pull of the earth. So the weight of the car is not 1200kg, but the mass is 1200kg. Many mistakes are often made with this.
Calculate axle load at the rear:
When the total weight and 1 axle load are known, it is very easy to calculate the 2nd axle load by subtracting these two:
Total weight – F2 = F1:
14715 – 6154 = 8561N.
F1 can of course also be calculated separately. This is almost the same as the first calculation:

14715 x 1,6 – F1 x 2,75 = 0
23544 – F1 x 2,75 = 0
F1 = 23544 / 2,75
F1 = 8561N
The force exerted by the front wheel on the road surface is 8561N and the rear wheel 6154N. Added together this is 14715N. The total vehicle mass is therefore 14715 / 9.81 = 1500kg.
Calculate bullet pressure:
In the same way as the axle loads on the car were calculated in the previous chapters, the nose weight on the towbar of the car can also be determined. Moment is force x arm. That is, the longer the arm is, the greater the moment becomes. The rear axle load depends on the distance between F2 and F3 and the nose weight depends on the distance between F3 and F4. And it is precisely the force on 'the pivot point', or the towball ball, that must be calculated.
The car is 1500kg, and the trailer 300kg. We first convert this to Newton by multiplying it by the gravitational acceleration:
1500 x 9,81 = 14715N
300 x 9,81 = 2943N
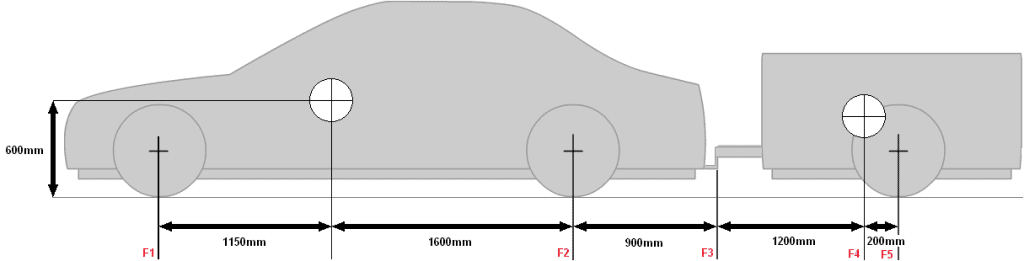
To calculate the nose weight it is easier to first only draw the trailer. The car itself is not important in the calculation.
The nose weight is indicated by F3 and the force with which the tire presses on the road surface F5.
F3 will be the pivot point and we are going to calculate the force F5. The center of gravity is a force downwards, so positive. The force acting on F5 is a force up, so it's negative (so it will have a minus sign in front of it). The weight of the trailer is 4000N.
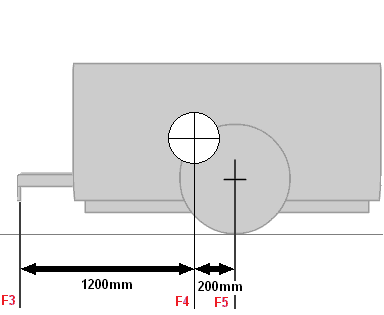
To calculate the force F5:
4000 x 1,2 – F5 x 1,4 = 0
4800 – F5 x 1,4 = 0
F5 = 4800 / 1,4
F5 = 3429N
To calculate the nose weight (F3):
4000 – 3429 = 571N
571 / 9,81 = 58,2kg
The nose weight with this trailer is 58,2 kg.
If the center of gravity moves backwards, the nose weight decreases. To gain this insight and to practice with the calculations, it is useful to increase and decrease the distance between F3 and F4 and therefore also between F4 and F5 and perform the calculation again.
Calculating the influence of the nose weight on the rear axle:
Because the nose weight is now known, it is possible to calculate what influence this has on the rear axle. The weight cannot simply be added, because the distance between the rear axle and the tow ball is of great importance (force x arm). We take the same image of the car with trailer again.

In the previous calculation it had become known that the nose weight (F3) is 571N. F2 was also known, that was 6154N. The forces cannot be added together, because the distance between the rear wheel and the head of the towbar ball still functions as an arm. We'll recreate the entire formula, like at the very beginning of this page. With this formula 571 x 3,65 is added (the force on F3 with the distance from F1 to F3 added).
14715 x 1,15 + 571 x 3,65 – F2 x 2,75 = 0
19006 – F2 x 2,75 = 0
F2 = 19006 / 2,75
F2 = 6911N = 691kg.
This means that the weight of the rear axle is 691 kg.
